معادله فیشر

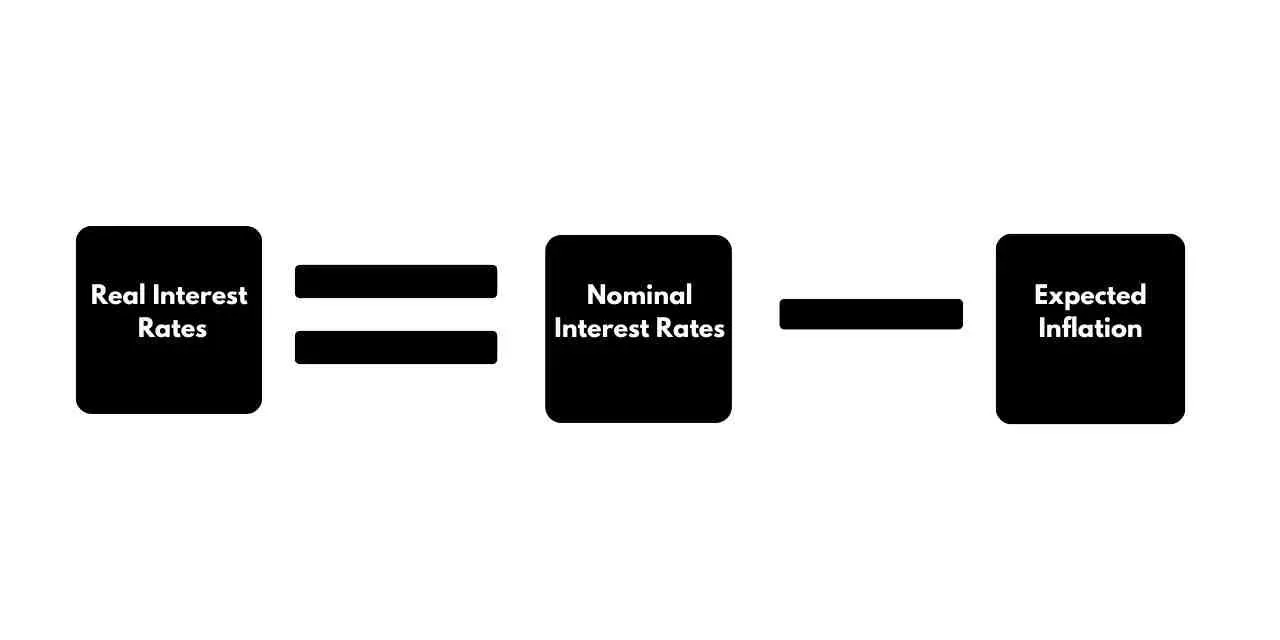
معادله فیشر که نخستین‌بار در سال 1930 توسط ایروینگ فیشر معرفی شد، یکی از نظریه‌های بنیادین و تأثیرگذار در اقتصاد پولی به شمار می‌رود. این معادله پیوندی منسجم میان نرخ بهره اسمی، نرخ بهره واقعی و نرخ تورم برقرار می‌کند و از همین‌رو، جایگاه مهمی در تحلیل‌های اقتصادی دارد.

اهمیت معادله فیشر تنها به سطح نظری محدود نمی‌شود، بلکه در عمل، نقشی کلیدی در تدوین سیاست‌های پولی، ارزیابی فرصت‌های سرمایه‌گذاری و تحلیل روندهای نرخ ارز ایفا می‌کند. امروزه این معادله به‌عنوان یکی از پایه‌های اساسی در اقتصاد کلان مدرن، به‌طور گسترده در میان بانک‌های مرکزی، نهادهای مالی و سرمایه‌گذاران مورد استفاده قرار می‌گیرد.

بیشتر بخوانید: اثر فیشر در مورد نرخ بهره اسمی

ایروینگ فیشر – معمار معادله فیشر

زندگینامه علمی

ایروینگ فیشر (Irving Fisher)، متولد 1867 و درگذشته در 1947، از برجسته‌ترین چهره‌های مکتب نئوکلاسیک و یکی از بنیان‌گذاران اقتصاد مدرن به‌شمار می‌رود. او تحصیلات خود را در دانشگاه ییل (Yale) گذراند و عنوان نخستین فردی را کسب کرد که موفق به دریافت دکترای اقتصاد از این دانشگاه شد.

فیشر نه‌تنها به‌واسطه معادله مشهور خود شناخته می‌شود، بلکه در زمینه‌های مهمی مانند نظریه سرمایه، قیمت‌گذاری دارایی‌ها، و طراحی شاخص‌های اقتصادی نیز دستاوردهای ماندگاری از خود بر جای گذاشت. جوزف شومپیتر، اقتصاددان برجسته اتریشی، او را “بزرگ‌ترین اقتصاددان آمریکایی” خوانده است؛ لقبی که گویای عمق نفوذ و اثرگذاری آثار علمی فیشر در سیر تحول علم اقتصاد است.

بیشتر بخوانید: اثر فیشر چیست؟

زمینه تاریخی کشف معادله

معادله فیشر در بستر تحولات فکری دهه 1930 و در پاسخ به یک پرسش بنیادین شکل گرفت: چرا در دوره‌های تورمی، نرخ‌های بهره اسمی افزایش می‌یابند؟ فیشر با دقتی بی‌نظیر تحلیل کرد که وام‌دهندگان برای حفظ قدرت خرید سرمایه خود، نیازمند جبران افت ارزش پول هستند.

از این‌رو، نرخ بهره اسمی باید بازتاب‌دهنده نرخ تورم باشد. بر این اساس، او رابطه‌ای فرمول‌بندی کرد که نشان می‌داد نرخ بهره اسمی برابر است با مجموع نرخ بهره واقعی و نرخ تورم مورد انتظار. این نظریه انقلابی، سنگ‌بنای درک مدرن از نرخ بهره واقعی تعدیل‌شده با تورم شد و جایگاهی اساسی در نظریه‌های پولی، سیاست‌گذاری اقتصادی و تحلیل‌های سرمایه‌گذاری یافت.

چرا معادله فیشر مهم است؟

اهمیت معادله فیشر از اینجا ناشی می‌شود که به ما کمک می‌کند بفهمیم «ارزش واقعی پول» در طول زمان چگونه تغییر می‌کند. این معادله برای سرمایه‌گذاران، بانک‌های مرکزی و حتی مردم عادی مثل یک قطب‌نما عمل می‌کند؛ نشان می‌دهد وقتی تورم بالا می‌رود، چطور باید نرخ بهره تنظیم شود تا قدرت خرید حفظ شود.

برای مثال، اگر تورم بالا برود ولی نرخ بهره ثابت بماند، در واقع بازده واقعی پول پایین می‌آید. یعنی با اینکه ظاهراً سود می‌گیرید، اما در عمل قدرت خرید شما کمتر می‌شود. بانک‌های مرکزی با استفاده از این معادله متوجه می‌شوند که اگر بخواهند تورم را کنترل کنند، باید نرخ بهره اسمی را هم بالا ببرند تا اقتصاد از مسیر خارج نشود.

در واقع، معادله فیشر به همه‌ی ما یادآوری می‌کند که در اقتصاد، ظاهر اعداد همیشه گویای حقیقت نیست—و آن‌چه اهمیت دارد، «واقعیت پشت ارقام» است.

کاربردهای معادله فیشر در اقتصاد و مالی

تحلیل سرمایه‌گذاری و اوراق قرضه

وقتی می‌خواهید بدانید یک سرمایه‌گذاری واقعاً چقدر سود دارد، نمی‌توانید فقط به عددی که بانک یا شرکت به شما می‌دهد (نرخ بهره اسمی) نگاه کنید. باید تورم را هم در نظر بگیرید.

مثلاً اگر سود سالانه شما 8 درصد باشد ولی قیمت‌ها 5 درصد افزایش پیدا کرده باشند، سود واقعی شما فقط 3 درصد است، چون با آن پول فقط 3 درصد بیشتر از قبل می‌توانید خرید کنید.

در بازار اوراق قرضه هم همین منطق وجود دارد. سرمایه‌گذاران حرفه‌ای با در نظر گرفتن تورم، ارزش واقعی سودی که دریافت می‌کنند را بررسی می‌کنند. حتی اختلاف‌های کوچک بین نرخ اسمی و نرخ واقعی در مقیاس سرمایه‌گذاری‌های میلیاردی می‌تواند تأثیر زیادی داشته باشد.

تحلیل هزینه فرصت

فرض کنید دو پروژه سرمایه‌گذاری پیش روی شماست. یکی ممکن است سود خوبی داشته باشد ولی در شرایطی که تورم بالا باشد، سود آن بی‌ارزش شود.

برای اینکه تصمیم درستی بگیرید، باید مشخص کنید کدام پروژه واقعاً برای شما به‌صرفه‌تر است. در اینجا، معادله فیشر کمک می‌کند تا بفهمید بعد از در نظر گرفتن تورم، هر پروژه چه بازده واقعی‌ای دارد.

جالب اینجاست که دو روش برای تحلیل وجود دارد: یا تورم را از همه محاسبات حذف می‌کنید، یا آن را در همه مراحل لحاظ می‌کنید — در هر دو صورت، اگر درست انجام شود، به یک نتیجه می‌رسید. این هماهنگی به لطف چارچوبی است که معادله فیشر فراهم می‌کند.

بیشتر بخوانید: هزینه فرصت چیست؟

سیاست‌گذاری پولی

بانک‌های مرکزی مثل فدرال رزرو آمریکا یا بانک مرکزی اروپا از این معادله برای طراحی سیاست‌های اقتصادی استفاده می‌کنند.

وقتی تورم زیاد می‌شود، بانک مرکزی نمی‌تواند نرخ بهره را ثابت نگه دارد. چون اگر نرخ بهره واقعی منفی شود (یعنی تورم از سود بانکی بیشتر شود)، مردم انگیزه‌ای برای پس‌انداز ندارند و ممکن است پول خود را صرف خرید کالا یا تبدیل به دارایی‌هایی مثل طلا کنند، که خودش تورم را بدتر می‌کند.

پس اگر بانک مرکزی بخواهد شرایط اقتصادی را کنترل کند، باید نرخ‌های اسمی را با توجه به تورم تغییر دهد — چیزی که دقیقاً در قلب معادله فیشر قرار دارد.

اقتصاد بین‌الملل

معادله فیشر در اقتصاد بین‌الملل نقش کلیدی دارد، چرا که به ما کمک می‌کند ارتباط بین نرخ بهره کشورها و نوسانات نرخ ارز را بهتر بفهمیم. این معادله اساس مفهوم مهمی به نام «پاریته نرخ بهره» (Interest Rate Parity) است که نشان می‌دهد تفاوت نرخ بهره در دو کشور چطور باید با تغییرات نرخ ارز متعادل شود.

وقتی نرخ تورم در یک کشور متفاوت با کشور دیگر باشد، نرخ بهره آن کشور نیز به همان نسبت تغییر می‌کند تا قدرت خرید و سرمایه‌گذاری حفظ شود. این فرایند باعث می‌شود نرخ ارزها بین کشورها نوسان کند و بازارهای مالی و تجارت جهانی به‌درستی تنظیم شوند.

بنابراین، معادله فیشر ابزاری حیاتی برای شرکت‌ها و سرمایه‌گذارانی است که در سطح بین‌المللی فعالیت می‌کنند، چون به آن‌ها کمک می‌کند تا ریسک‌های ناشی از تغییرات نرخ ارز و تورم را بهتر مدیریت کنند و تصمیمات اقتصادی دقیق‌تری بگیرند.

تشریح ریاضی معادله فیشر

فرم‌های اصلی معادله

معادله فیشر در دو قالب اصلی ارائه می‌شود که هر یک برای اهداف تحلیلی یا محاسباتی خاصی کاربرد دارد:

فرم تقریبی (شکل رایج در تحلیل‌های اولیه):

i ≈ r + π

در این رابطه:

• i: نرخ بهره اسمی
• $r$: نرخ بهره واقعی
• $\pi$: نرخ تورم مورد انتظار

این نسخه برای تحلیل‌های مفهومی و بررسی‌های نظری اولیه مناسب است، چرا که رابطه‌ای ساده و خطی ارائه می‌دهد.

فرم دقیق (مرجع در محاسبات مالی):

r + 1 = (π +r ) (1 + 1)

این نسخه اثرات مرکب تورم و بهره را لحاظ می‌کند و در محاسبات دقیق مالی، مانند ارزش فعلی اوراق قرضه، محاسبه نرخ بازده مؤثر و برنامه‌ریزی مالی بلندمدت، ضروری است.

استخراج ریاضی معادله

برای درک عمیق‌تر، فرض کنیم فردی در زمان t یک ورقه قرضه به مبلغ 1 دلار با نرخ بهره اسمی i_t خریداری می‌کند. ارزش واقعی پولی که در پایان دوره دریافت می‌کند، پس از تعدیل با تورم دوره $t+1$، به‌صورت زیر محاسبه می‌شود:

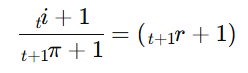
که در آن:

• _t+1r: نرخ بهره واقعی در دوره t+1

• _1+tπ​: نرخ تورم مورد انتظار برای دوره t+1

با بازآرایی این رابطه:

گسترش سمت راست معادله:

چون حاصل‌ضرب r_t+1​_⋅π_t+1​ در اغلب موارد عددی بسیار کوچک است (برای مثال اگر هر کدام 5٪ باشند، حاصل‌ضرب آن‌ها 0٫0025 یا 0٫25٪ است)، این جمله را در کاربردهای تحلیلی حذف می‌کنند تا به شکل تقریبی معادله برسند:

i ≈ r + π

تابعیت نرخ بهره واقعی

با تبدیل معادله، می‌توان نرخ بهره واقعی را نیز به‌سادگی برآورد کرد:

i ≈ π – r

به‌عبارت دیگر، نرخ بهره واقعی، نرخ سودی است که پس از تعدیل اثر تورم باقی می‌ماند.

مثال کاربردی:

فرض کنید بانک، سپرده‌ای با نرخ بهره اسمی 8٪ ارائه می‌دهد و نرخ تورم سالانه نیز 5٪ است. در این صورت، نرخ بهره واقعی چنین محاسبه می‌شود:

r ≈ 8% − 5% = 3%

یعنی قدرت خرید واقعی سرمایه‌گذار فقط 3٪ افزایش می‌یابد، نه 8٪. این تفاوت برای تصمیم‌گیری مالی و سرمایه‌گذاری بسیار حیاتی است، زیرا نرخ بهره واقعی نشان‌دهنده بازده واقعی سرمایه پس از اثرات تورمی است.

پیشرفت‌های ریاضی و حل معادله فیشر

مدل‌سازی انتظارات تورمی

یکی از مهم‌ترین پیشرفت‌ها در زمینه معادله فیشر، جایگزینی «تورم واقعی» با «تورم انتظاری» است. به‌جای آن‌که بگوییم نرخ بهره اسمی به تورمی وابسته است که در گذشته رخ داده، می‌گوییم نرخ بهره به تورمی وابسته است که مردم انتظار دارند در آینده اتفاق بیفتد.

این تغییر ساده اما مهم، باعث شد معادله فیشر نه‌فقط ابزاری برای تحلیل گذشته، بلکه ابزاری برای پیش‌بینی آینده در بازارهای مالی و سیاست‌گذاری پولی شود. به‌همین دلیل، تحلیل‌گران و بانک‌های مرکزی اکنون از نسخه‌ای از معادله فیشر استفاده می‌کنند که در آن «انتظارات تورمی» نقش کلیدی دارد.

مثلاً اگر بازار انتظار داشته باشد که تورم بالا برود، حتی اگر هنوز تورم واقعی تغییری نکرده باشد، نرخ بهره اسمی افزایش پیدا می‌کند. این به معنای نقش روانی و آینده‌نگر در بازارهای مالی است.

حل عددی و روش‌های ریاضی پیشرفته

معادله فیشر در حالت معمولی‌اش بسیار ساده است، اما وقتی وارد شرایط واقعی‌تر می‌شویم، مثل نوسانات سریع نرخ تورم یا بازده‌های متغیر، دیگر با یک معادله ساده طرف نیستیم. در این شرایط، ریاضی‌دانان و اقتصاددانان از روش‌های عددی و کامپیوتری استفاده می‌کنند تا راه‌حل‌هایی دقیق‌تر به دست آورند.

برای مثال، در یک مقاله علمی که در سال 1398 منتشر شد، پژوهشگران ایرانی از تکنیکی به‌نام «توابع پایه متعامد» (مثل توابع ژاکوبی) برای حل نسخه غیرخطی معادله فیشر استفاده کردند. این تکنیک‌ها به آن‌ها کمک کرد که دقیق‌تر مدل‌سازی کنند که چگونه تورم می‌تواند قدرت خرید مردم و بازده سرمایه‌گذاری‌ها را تحت تأثیر قرار دهد.

به زبان ساده‌تر، وقتی شرایط بازار پیچیده می‌شود (مثلاً نرخ تورم بالا و متغیر است، یا بازده سرمایه‌گذاری‌ها نوسانی است)، برای تحلیل دقیق اثر تورم بر سرمایه‌گذاری‌ها، دیگر نمی‌توان از معادله‌های سرراست استفاده کرد و باید سراغ ابزارهای پیشرفته‌تر رفت.

اثر فیشر بین‌المللی (IFE)

اثر فیشر بین‌المللی، در واقع همان منطق معادله فیشر را به دنیای اقتصاد بین‌الملل گسترش می‌دهد. این نظریه می‌گوید که تفاوت نرخ بهره بین دو کشور، می‌تواند تغییرات نرخ ارز میان آن‌ها را پیش‌بینی کند.

اگر کشوری نرخ بهره بالاتری داشته باشد، احتمال دارد که ارزش پولش در آینده کاهش یابد. دلیلش این است که با نرخ بهره بالا، مردم تمایل دارند پول قرض بگیرند و خرج کنند، که ممکن است به افزایش تورم و در نتیجه کاهش ارزش پول منجر شود.

پیش‌بینی نرخ ارز با استفاده از IFE

فرض کنید نرخ بهره در آمریکا 5 درصد و در ژاپن تنها 0.1 درصد است. با توجه به اثر فیشر بین‌المللی، انتظار می‌رود که دلار آمریکا نسبت به ین ژاپن در آینده تضعیف شود.
چرا؟ چون سرمایه‌گذاران انتظار دارند که نرخ بهره بالاتر در آمریکا در بلندمدت به کاهش ارزش دلار منجر شود.

به‌عبارت دیگر، اگر شما الان دلار بخرید چون نرخ بهره‌اش بالاست، ممکن است سال آینده وقتی می‌خواهید دلارهایتان را به ین تبدیل کنید، ببینید که دلار ضعیف‌تر شده و سود شما کمتر از انتظار بوده.

محدودیت‌های نظریه

البته این نظریه هم مثل همه نظریه‌های اقتصادی، فرض‌هایی دارد که همیشه در دنیای واقعی برقرار نیستند:

• جریان آزاد سرمایه: فرض بر این است که پول می‌تواند آزادانه بین کشورها جابه‌جا شود. اما در بسیاری از کشورها، کنترل‌های ارزی وجود دارد که مانع از جریان آزاد سرمایه می‌شود.
• ریسک‌های سیاسی: اتفاقاتی مثل بی‌ثباتی سیاسی، تحریم یا بحران‌های مالی می‌توانند بازار ارز را به‌کلی دگرگون کنند و پیش‌بینی‌های مبتنی بر نرخ بهره را بی‌اعتبار سازند.
• عوامل کوتاه‌مدت: در کوتاه‌مدت، نرخ ارز بیشتر تحت‌تأثیر عوامل روانی، اخبار، سفته‌بازی یا تصمیمات ناگهانی سرمایه‌گذاران قرار دارد و ممکن است دقیقاً برخلاف چیزی حرکت کند که اثر فیشر پیش‌بینی کرده بود.

در مجموع، اثر فیشر بین‌المللی یک ابزار مفید برای درک رابطه میان نرخ بهره و نرخ ارز در بلندمدت است، اما نباید به‌تنهایی و بدون در نظر گرفتن عوامل سیاسی، روانی و ساختاری از آن برای پیش‌بینی دقیق بازار ارز استفاده کرد.

پارادوکس‌ها و محدودیت‌های معادله فیشر

تله نقدینگی

یکی از معروف‌ترین شرایطی که معادله فیشر در آن دچار چالش می‌شود، چیزی است که اقتصاددان‌ها به آن می‌گویند «تله نقدینگی». در این وضعیت، نرخ بهره اسمی تقریباً صفر یا حتی منفی می‌شود—اما مردم هنوز علاقه‌ای به خرج کردن پول ندارند.

چرا؟ چون تورم هم منفی شده و ارزش پول در حال افزایش است. پس افراد ترجیح می‌دهند پولشان را نگه دارند و خرج نکنند، چون فکر می‌کنند بعداً با همان مقدار پول می‌توانند چیزهای بیشتری بخرند.

این اتفاق دقیقاً در ژاپن دهه 1990 افتاد. با وجود نرخ بهره پایین، اقتصاد در رکود ماند، چون مردم خرج نمی‌کردند. این تناقض باعث شد که اقتصاددان‌ها متوجه شوند فقط پایین بودن نرخ بهره برای تحریک اقتصاد کافی نیست.

اثر انتظارات و سرعت واکنش بازار

معادله فیشر بر اساس این فرض است که انتظارات مردم درباره تورم با یک وقفه زمانی تغییر می‌کند؛ یعنی اگر تورم بالا برود، مردم مدتی بعد متوجه می‌شوند و نرخ‌های بهره را تنظیم می‌کنند. اما در دنیای واقعی، مخصوصاً در کشورهای با تورم بالا، مردم بسیار سریع واکنش نشان می‌دهند.

مثلاً در کشورهایی مثل آرژانتین یا ونزوئلا که تورم بالا و ناپایدار دارند، نرخ‌های بهره اسمی به سرعت بالا می‌رود چون همه می‌دانند که ارزش پول در حال کاهش است. در نتیجه، فرض «واکنش کند» که در نظریه اصلی فیشر آمده، همیشه درست از آب درنمی‌آید.

تأثیر ریسک و مالیات

نکته مهم دیگری که در معادله فیشر به‌سادگی از قلم افتاده، ریسک و مالیات است. این معادله فرض می‌کند که شما دارید در یک بازار کاملاً امن سرمایه‌گذاری می‌کنید، اما در واقعیت، سرمایه‌گذاری‌ها معمولاً ریسک دارند.

هرچه یک دارایی ریسک بیشتری داشته باشد، سرمایه‌گذار انتظار دارد بازده بیشتری بگیرد.

از طرف دیگر، مالیات هم نقش مهمی بازی می‌کند. اگر دولت روی سود اسمی مالیات ببندد (مثلاً شما 8٪ سود گرفته‌اید ولی باید 2٪ مالیات بدهید)، در عمل چیزی که به‌صورت واقعی نصیب شما می‌شود بسیار کمتر است. بنابراین معادله فیشر برای تحلیل دقیق بازده واقعی، باید این عوامل را هم در نظر بگیرد—اما نسخه کلاسیک آن چنین نمی‌کند.

تأثیر معادله فیشر بر مطالعات مدرن

بازگشت نظریه در بحران مالی 2008

در دوران رکود بزرگ سال 2008، بسیاری از نظریه‌های کلاسیک دوباره روی میز تحلیل‌گران اقتصادی آمدند. یکی از این نظریه‌ها، دیدگاه اروینگ فیشر درباره «کاهش قیمت بدهی» یا همان Debt Deflation بود. به‌طور ساده، فیشر هشدار داده بود که اگر قیمت‌ها در اقتصاد شروع به کاهش کنند، بدهی‌های مردم و شرکت‌ها که به‌صورت عددی و اسمی ثابت هستند، سنگین‌تر و سنگین‌تر به‌نظر می‌رسند.

برای مثال، فرض کن شما باید 100 دلار بدهی پس بدهی، ولی به‌خاطر کاهش قیمت‌ها، درآمد شما کمتر شده یا ارزش پول بیشتر شده—در نتیجه بازپرداخت آن 100 دلار سخت‌تر از قبل می‌شود.

این اتفاق باعث می‌شود مردم دچار ناتوانی در پرداخت بدهی شوند و موجی از ورشکستگی راه بیفتد. این تحلیل فیشر در بحران 2008 به‌شدت مورد توجه اقتصاددان‌ها قرار گرفت، چون شباهت زیادی با شرایط آن زمان داشت.

پیوند با نظریه‌های پولی جدید

میلتون فریدمن، یکی از چهره‌های اصلی مکتب پول‌گرایی (Monetarism)، از ایده‌های فیشر الهام گرفت. او به نقش پول در ایجاد تورم تاکید داشت و معادله فیشر را به‌عنوان پایه‌ای برای توضیح رابطه بین عرضه پول و سطح قیمت‌ها به‌کار برد.

در اینجا، تمرکز روی این بود که اگر پول در گردش زیاد شود ولی حجم کالاها و خدمات تغییر نکند، قیمت‌ها بالا می‌رود—یعنی تورم رخ می‌دهد. این دیدگاه تأثیر زیادی بر سیاست‌های پولی در دهه‌های 1970 و 1980 گذاشت و بانک‌های مرکزی را به کنترل رشد نقدینگی ترغیب کرد.

توسعه ابزارهای مالی بر پایه تورم

یکی از دستاوردهای عملی معادله فیشر در دنیای امروز، خلق ابزارهایی است که تورم را مستقیماً در نظر می‌گیرند:

• اوراق بهادار مبتنی بر تورم (مثل TIPS در آمریکا): این اوراق طوری طراحی شده‌اند که از قدرت خرید سرمایه‌گذار در برابر تورم محافظت کنند. سود این اوراق با توجه به نرخ تورم تنظیم می‌شود، طوری‌که سرمایه‌گذار در هر شرایطی، بازده واقعی خودش را حفظ کند.
• سوآپ تورمی (Inflation Swap): این ابزار نوعی قرارداد مالی است که به شرکت‌ها و سرمایه‌گذاران کمک می‌کند ریسک ناشی از تغییرات تورم را مدیریت کنند. مثلاً اگر یک شرکت نگران افزایش قیمت‌ها در سال‌های آینده باشد، می‌تواند با یک طرف دیگر معامله کند تا در صورت بالا رفتن تورم، خسارتش جبران شود.

نتیجه گیری

معادله فیشر شاید در نگاه اول فقط یک رابطه ساده بین نرخ بهره، تورم و بازده واقعی به‌نظر برسد، اما در واقع، چیزی فراتر از یک فرمول است. این معادله مثل پلی عمل می‌کند؛ پلی که از یک‌سو به سیاست‌گذاران اقتصادی کمک می‌کند تصمیم‌های درست بگیرند، و از سوی دیگر به سرمایه‌گذاران و حتی مردم عادی درک بهتری از آینده مالی‌شان می‌دهد.

در دنیای پیچیده امروز، جایی که بانک‌های مرکزی هم‌زمان باید با تورم بجنگند و جلوی رکود را بگیرند، فهم درست این معادله به یک ابزار ضروری تبدیل شده است—نه فقط برای اقتصاددانان، بلکه برای هر کسی که با پول سر و کار دارد.

علاوه بر این، پیشرفت‌های علمی و محاسباتی باعث شده‌اند که معادله فیشر به یک ابزار دقیق‌تر تبدیل شود. مثلاً استفاده از روش‌های پیچیده ریاضی مثل پایه‌های متعامد یا نظریه‌های مربوط به انتظارات عقلانی، به تحلیل‌گران این امکان را داده تا آینده اقتصاد را با دقت بیشتری پیش‌بینی کنند.

در نهایت، می‌توان گفت میراث فیشر فقط یک فرمول نیست، بلکه زبانی جهانی برای فهم پیچیدگی‌های اقتصاد پولی است—زبانی که هنوز زنده است و همچنان حرف‌های زیادی برای گفتن دارد.