میانگین ها در اقتصاد

میانگین ها در اقتصاد به عنوان یکی از مهم‌ترین مفاهیم آماری، نقش محوری در تحلیل داده‌ها و تصمیم‌گیری در حوزه‌های مختلف، ایفا می‌کنند. در اقتصاد، میانگین‌ها به عنوان نماینده‌ای از یک مجموعه داده، به ما کمک می‌کنند تا به طور خلاصه و دقیق، اطلاعات پیچیده را درک و تفسیر کنیم.

از محاسبه‌ی متوسط درآمد ملی گرفته تا مقایسه‌ی نرخ بیکاری در کشورهای مختلف، میانگین‌ها به عنوان ابزاری قدرتمند برای توصیف، تحلیل و پیش‌بینی پدیده‌های اقتصادی به کار می‌روند.

ویدئو آموزشی مرتبط با این مطلب

کاربرد میانگین ها در اقتصاد

تحلیل درآمد و توزیع ثروت

یکی از کاربردهای مهم میانگین‌ها، بررسی درآمد و توزیع ثروت در یک جامعه است. میانگین درآمد به ما نشان می‌دهد که به طور کلی وضعیت اقتصادی یک گروه از افراد چگونه است. اما این عدد همیشه نمایانگر نابرابری‌ها نیست. به عنوان مثال، اگر چند نفر در یک جامعه درآمد بسیار بالایی داشته باشند، میانگین درآمد ممکن است وضعیت را بهتر از آنچه که برای افراد کم‌درآمد وجود دارد، نشان دهد. در چنین شرایطی، استفاده از میانگین‌های دیگر مانند میانه (که درآمد وسط را نشان می‌دهد) یا مد (که پرتکرارترین درآمد را نشان می‌دهد) می‌تواند تصویر دقیق‌تری از توزیع واقعی درآمد ارائه دهد.

اندازه‌گیری تولید و بهره‌وری

میانگین‌ها در ارزیابی تولید و بهره‌وری صنایع مختلف نقش مهمی دارند. برای مثال، میانگین تولید یک کارخانه در یک دوره زمانی مشخص می‌تواند به مدیران کمک کند تا بدانند عملکرد کارخانه در طول زمان چگونه بوده است. این اطلاعات به آن‌ها در تصمیم‌گیری بهتر کمک می‌کند. همچنین، با استفاده از میانگین تولید، می‌توان عملکرد کارخانه‌های مختلف یا صنایع را با هم مقایسه کرد.

اندازه‌گیری نابرابری

برای تحلیل نابرابری‌های اقتصادی، میانگین‌ها نقش مهمی ایفا می‌کنند. به‌ویژه میانه و ضریب جینی، ابزارهای کلیدی برای اندازه‌گیری توزیع درآمد و ثروت در جامعه هستند. میانه (Median) نشان می‌دهد که نیمی از افراد جامعه درآمدی بالاتر و نیمی درآمدی پایین‌تر از یک مقدار خاص دارند، که این شاخص به‌خصوص در جوامعی با نابرابری شدید کاربرد دارد. ضریب جینی نیز به بررسی نابرابری توزیع درآمد کمک می‌کند و به سیاست‌گذاران نشان می‌دهد که آیا سیاست‌های اقتصادی منجر به کاهش یا افزایش نابرابری در جامعه شده‌اند.

تحلیل رگرسیون

در تحلیل رگرسیون، میانگین‌ها برای محاسبه ضرایب استفاده می‌شوند. این ضرایب به ما نشان می‌دهند که هر عامل ورودی، مثل قیمت یا هزینه، چه تأثیری بر نتیجه‌ای مانند تقاضا یا فروش دارد. با استفاده از این روش، تحلیل‌گر می‌تواند رابطه میان عوامل مختلف و نتایج آن‌ها را بهتر درک کند. تحلیل رگرسیون یکی از ابزارهای کلیدی در اقتصاد است که به اقتصاددانان کمک می‌کند تأثیر سیاست‌ها و تصمیمات مختلف را بر روی متغیرهای اقتصادی بسنجند و از این نتایج برای سیاست‌گذاری‌های بهتر استفاده کنند.

پیش‌بینی و مدل‌سازی اقتصادی

در پیش‌بینی رفتارهای اقتصادی، میانگین‌ها نقش کلیدی دارند. به عنوان نمونه، در مدل‌های اقتصادی از میانگین داده‌های تاریخی استفاده می‌شود تا روندهای آینده را پیش‌بینی کنند. این نوع پیش‌بینی به سیاست‌گذاران کمک می‌کند که تصمیمات بهتری برای مدیریت اقتصاد بگیرند.

ارزیابی سیاست‌های اقتصادی

میانگین‌ها در ارزیابی سیاست‌های اقتصادی نقش مهمی دارند. برای مثال، اگر یک برنامه برای کاهش بیکاری اجرا شود، می‌توان از میانگین نرخ بیکاری برای سنجیدن موفقیت آن برنامه استفاده کرد. اگر میانگین نرخ بیکاری پس از اجرای برنامه کاهش یابد، نشان‌دهنده این است که برنامه مؤثر بوده است. به همین ترتیب، از میانگین‌ها می‌توان برای ارزیابی نتایج سایر سیاست‌های اقتصادی نیز استفاده کرد.

تحلیل سری‌های زمانی

در تحلیل سری‌های زمانی، از میانگین‌های متحرک برای شناسایی روندهای کلی و تغییرات دوره‌ای استفاده می‌شود. میانگین متحرک به این صورت عمل می‌کند که برای هر نقطه در زمان، میانگین داده‌های قبلی (مثلاً 3 یا 6 ماه گذشته) محاسبه می‌شود و این به تحلیلگر کمک می‌کند تا نوسانات کوتاه‌مدت را حذف کرده و بر روندهای بلندمدت تمرکز کند. به‌عنوان مثال، در تحلیل نرخ تورم یا رشد اقتصادی، استفاده از میانگین‌های متحرک کمک می‌کند تا روندهای کلی اقتصاد را بهتر مشاهده کنیم و از نوسانات روزمره و کوتاه‌مدت اجتناب کنیم.

مقایسه‌ی گروه‌ها

یکی دیگر از کاربردهای میانگین‌ها در اقتصاد، مقایسه‌ی گروه‌های مختلف است. با محاسبه‌ی میانگین درآمد، مصرف یا هر متغیر اقتصادی دیگر برای گروه‌های مختلف (مانند مناطق جغرافیایی یا گروه‌های سنی) می‌توان تفاوت‌ها و شباهت‌ها را شناسایی کرد. به‌عنوان مثال، میانگین درآمد در مناطق شهری ممکن است بالاتر از مناطق روستایی باشد و این مقایسه‌ها به سیاست‌گذاران کمک می‌کند تا نیازهای هر گروه را بهتر درک کرده و سیاست‌های حمایتی یا اصلاحی طراحی کنند.

چالش ها و محدودیت های میانگین ها در اقتصاد

نابرابری و مخفی کردن تفاوت‌ها

یکی از مشکلات اصلی استفاده از میانگین‌ها این است که می‌توانند نابرابری‌ها را پنهان کنند. میانگین فقط یک عدد کلی را نشان می‌دهد و ممکن است تفاوت‌های مهم بین افراد را نشان ندهد. برای مثال، در جامعه‌ای که تعداد کمی افراد خیلی ثروتمند و تعداد زیادی افراد کم‌درآمد هستند، میانگین درآمد ممکن است بالا به نظر برسد، اما این رقم واقعیت شرایط افراد با درآمد کمتر را منعکس نمی‌کند.

راه‌حل: برای حل این مشکل، می‌توان از روش‌های دیگری مانند میانه و مد استفاده کرد. میانه نشان می‌دهد که نصف جامعه درآمدی بالاتر و نصف دیگر درآمدی کمتر از یک مقدار خاص دارند، و مد به ما می‌گوید که کدام مقدار بیشتر از همه تکرار شده است. این شاخص‌ها تصویر دقیق‌تری از وضعیت واقعی توزیع درآمد در جامعه به ما می‌دهند.

وابستگی به داده‌های دقیق

داده‌های نادرست یا ناقص می‌توانند به شدت بر میانگیـن ها تأثیر بگذارند. اگر داده‌ها به درستی جمع‌آوری نشوند یا به‌روز نباشند، میانگیـن به جای نشان دادن تصویر واقعی، ممکن است نتایج نادرستی ارائه کند. برای مثال، اگر اطلاعات مربوط به درآمد افراد با درآمد پایین به دقت ثبت نشود یا به‌روزرسانی نشود، میانگیـن نهایی نمی‌تواند بازتاب دقیقی از وضعیت اقتصادی جامعه باشد.

راه‌حل: سیاست‌گذاران و تحلیل‌گران باید به دقت داده‌ها توجه ویژه‌ای داشته باشند. استفاده از روش‌های مناسب برای جمع‌آوری داده‌ها، اطمینان از صحت اطلاعات، و انجام تحلیل‌های آماری که احتمال خطاها را در نظر می‌گیرند، می‌تواند به کاهش این مشکل کمک کند و نتایج بهتری ارائه دهد.

تفسیر نادرست نتایج

یکی از مشکلات استفاده از میانگیـن ها این است که گاهی به اشتباه به‌عنوان یک معیار دقیق و کامل در نظر گرفته می‌شوند. میانگین تنها یک تصویر کلی از داده‌ها ارائه می‌دهد و ممکن است واقعیت‌های پشت آن را پنهان کند. به‌عنوان مثال، اگر میانگیـن درآمد جامعه بالا باشد، این به معنی آن نیست که همه افراد از وضعیت خوبی برخوردار هستند؛ بلکه ممکن است تعدادی از افراد درآمد بسیار بالایی داشته باشند و باقی افراد در وضعیت نامناسبی باشند.

راه‌حل: تحلیل‌گران باید با دقت و احتیاط به تفسیر میانگیـن ها بپردازند. استفاده از ابزارهای آماری دیگر مانند انحراف معیار، که نشان‌دهنده میزان پراکندگی داده‌هاست، می‌تواند کمک کند تا تصویری دقیق‌تر از واقعیت ارائه شود. همچنین، باید به این نکته توجه داشت که میانگیـن فقط یک نما است و نباید از دیگر اطلاعات موجود در داده‌ها غافل شد.

اثر مقادیر افراطی (Outliers)

مقادیر خیلی متفاوت، یعنی داده‌هایی که به شدت با بقیه تفاوت دارند، می‌توانند میانگین را به شدت تحت تأثیر قرار دهند. مثلاً در تحلیل درآمد، اگر یک نفر درآمد بسیار بالایی داشته باشد، می‌تواند میانگیـن درآمد کل جامعه را زیاد کند، در حالی که اکثر مردم درآمد کمتری دارند.

راه‌حل: برای جلوگیری از تأثیر زیاد این مقادیر، می‌توان داده‌های خیلی متفاوت را حذف کرد یا از شاخص‌هایی مثل میانه استفاده کرد که کمتر تحت تأثیر این مقادیر قرار می‌گیرند. این کار کمک می‌کند تا تصویری واقعی‌تر از وضعیت کلی داده‌ها به دست آید.

زمان‌بر بودن جمع‌آوری داده‌ها

در برخی مواقع، جمع‌آوری داده‌های کافی و دقیق ممکن است زمان‌بر باشد. در این شرایط، سیاست‌گذاران ممکن است تحت فشار قرار بگیرند و نتوانند برای دریافت داده‌های دقیق صبر کنند. این موضوع به‌ویژه در مواقع بحران یا شرایط اضطراری اهمیت دارد، جایی که نیاز به تصمیم‌گیری سریع احساس می‌شود.

راه‌حل: در این مواقع، استفاده از داده‌های جزئی‌تر یا حتی تخمین‌های منطقی می‌تواند کمک‌کننده باشد. سیاست‌گذاران باید به اهمیت داده‌های سریع و قابل اعتماد توجه کنند و از مدل‌های آماری سریع برای تصمیم‌گیری‌های موقت استفاده کنند، تا زمانی که داده‌های دقیق‌تر در دسترس قرار گیرد.

انواع میانگین ها در اقتصاد

میانگین حسابی

میانگین حسابی ساده‌ترین و متداول‌ترین نوع میانگین است که برای محاسبه آن، همه مقادیر را با هم جمع کرده و سپس بر تعداد آن‌ها تقسیم می‌کنیم. این نوع میانگیـن به ما تصویری کلی از وضعیت ارائه می‌دهد. به عنوان مثال، اگر درآمد سالانه ۵ نفر به ترتیب ۴۰، ۵۰، ۶۰، ۷۰ و ۸۰ میلیون تومان باشد، برای محاسبه میانگیـن، ابتدا این اعداد را با هم جمع می‌کنیم و سپس مجموع را بر تعداد افراد (۵ نفر) تقسیم می‌کنیم که نتیجه آن ۶۰ میلیون تومان خواهد شد.

میانگین وزنی

میانگین وزنی زمانی استفاده می‌شود که مقادیر مختلف اهمیت یا وزن‌های متفاوتی دارند. این نوع میانگیـن به مقادیر مهم‌تر وزن بیشتری می‌دهد. مثلاً اگر بخواهیم میانگیـن هزینه‌های زندگی در مناطق مختلف را محاسبه کنیم، ممکن است هزینه‌های مناطق پرجمعیت‌تر را با وزن بیشتری در نظر بگیریم چون تعداد بیشتری از افراد در آن مناطق زندگی می‌کنند.

میانگین هندسی

میانگیـن هندسی زمانی استفاده می‌شود که بخواهیم نرخ‌های رشد یا درصد تغییرات را بررسی کنیم. این میانگین به طور خاص در زمانی مفید است که داده‌ها به صورت نسبی ارائه می‌شوند، مانند درصد رشد یا نرخ بهره. به جای جمع کردن اعداد، آن‌ها را در هم ضرب کرده و سپس ریشه‌ای از حاصل‌ضرب می‌گیریم.

میانگین هارمونیک

میانگیـن هارمونیک معمولاً در محاسبات نرخ‌ها به کار می‌رود. این نوع میانگین به‌ویژه برای مقادیر مربوط به نرخ‌ها، مانند نرخ بهره یا بازده‌های مالی، استفاده می‌شود. برای محاسبه این میانگین، به جای جمع کردن خود مقادیر، معکوس آن‌ها را جمع می‌کنیم و سپس معکوس مجموع را به دست می‌آوریم.

ویدئو آموزشی مرتبط با این مطلب

نحوه محاسبه انواع میانگین ها در اقتصاد

محاسبه میانگین حسابی

• جمع مقادیر: ابتدا همه مقادیر را با هم جمع می‌کنیم.
• تقسیم بر تعداد مقادیر: سپس مجموع به‌دست آمده را بر تعداد مقادیر تقسیم می‌کنیم.

مثال: اگر درآمد سالانه ۵ نفر به ترتیب ۴۰، ۵۰، ۶۰، ۷۰ و ۸۰ میلیون تومان باشد، برای محاسبه میانگین حسابی، ابتدا مجموع درآمدها را محاسبه می‌کنیم:

$$\mathrm{۴۰}+\mathrm{۵۰}+\mathrm{۶۰}+\mathrm{۷۰}+\mathrm{۸۰}=\mathrm{۳۰۰}\text{ میلیون تومان}$$

سپس این مجموع را بر تعداد افراد (۵ نفر) تقسیم می‌کنیم:

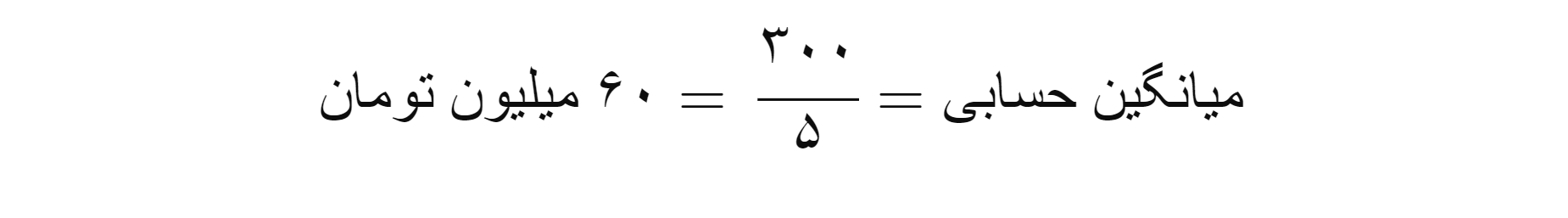
این میانگین به ما نشان می‌دهد که به طور میانگیـن هر فرد ۶۰ میلیون تومان درآمد دارد.

محاسبه میانگین وزنی

• ضرب مقادیر در وزن‌هایشان: هر مقدار را در وزن مربوط به آن ضرب می‌کنیم.
• جمع کردن حاصل‌ضرب‌ها: مجموع حاصل‌ضرب‌ها را محاسبه می‌کنیم.
• تقسیم بر مجموع وزن‌ها: این مجموع را بر مجموع وزن‌ها تقسیم می‌کنیم.

مثال: فرض کنید برای محاسبه میانگیـن هزینه‌های زندگی در دو منطقه، هزینه‌های زندگی در منطقه A (۱۰۰ میلیون تومان) و منطقه B (۲۰۰ میلیون تومان) به وزن‌های ۲ و ۳ به ترتیب مربوط می‌شود. محاسبه به شکل زیر است:

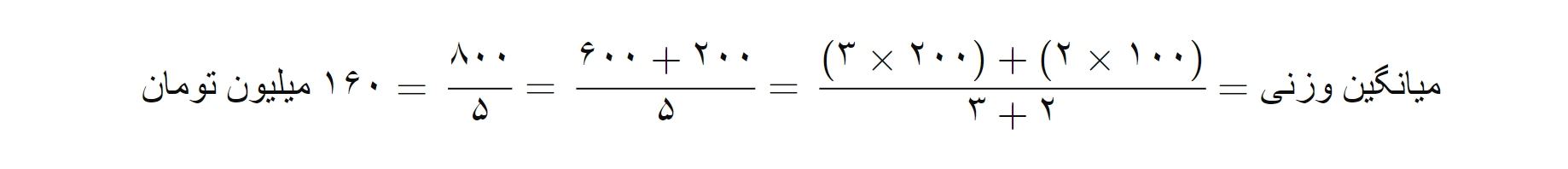
در این مثال، میانگین وزنی هزینه‌های زندگی ۱۶۰ میلیون تومان است.

محاسبه میانگین هندسی

برای محاسبه میانگیـن هندسی، مراحل زیر انجام می‌شود:

• ضرب مقادیر در هم: تمام مقادیر را در هم ضرب می‌کنیم.
• گرفتن ریشه nام: سپس ریشه nام این حاصل‌ضرب را محاسبه می‌کنیم.

مثال: فرض کنید نرخ رشد یک سرمایه‌گذاری به ترتیب ۱۰%، ۲۰% و ۳۰% باشد. برای محاسبه میانگیـن هندسی، ابتدا این نرخ‌ها را به نسبت‌های معادل تبدیل می‌کنیم:

• ۱۰% = 1.10
• ۲۰% = 1.20
• ۳۰% = 1.30

حاصل‌ضرب این نسبت‌ها:

$$1.10\times 1.20\times 1.30=1.56$$

حالا ریشه سوم این عدد را محاسبه می‌کنیم:

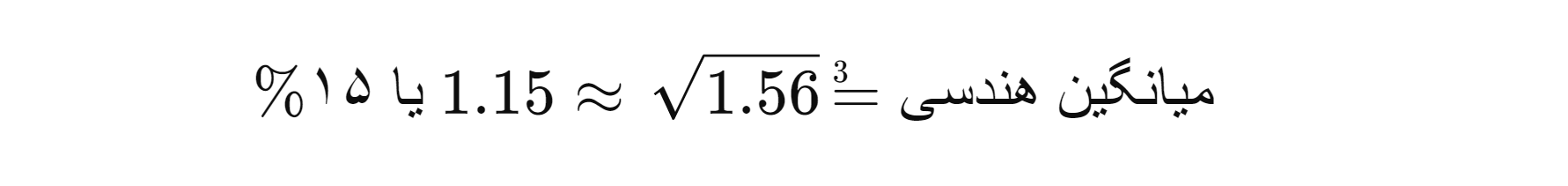
این نشان می‌دهد که میانگیـن نرخ رشد سرمایه‌گذاری تقریباً ۱۵% است.

محاسبه میانگین هارمونیک

• محاسبه معکوس مقادیر: ابتدا معکوس هر مقدار را محاسبه می‌کنیم.
• جمع کردن معکوس‌ها: سپس تمام معکوس‌ها را جمع می‌کنیم.
• تقسیم بر تعداد مقادیر: در نهایت، تعداد مقادیر را بر روی ۱ تقسیم بر مجموع معکوس‌ها می‌گذاریم.

مثال: فرض کنید نرخ بهره در دو سال به ترتیب ۱۰% و ۲۰% باشد. برای محاسبه میانگیـن هارمونیک:

1. نرخ‌ها را به صورت معکوس محاسبه می‌کنیم:

• ۱۰% = 0.10 → معکوس = 10
• ۲۰% = 0.20 → معکوس = 5

2. معکوس‌ها را جمع می‌کنیم:

$$10+5=15$$

3. در نهایت، تعداد مقادیر (۲) را بر روی ۱ تقسیم بر مجموع معکوس‌ها می‌گذاریم:

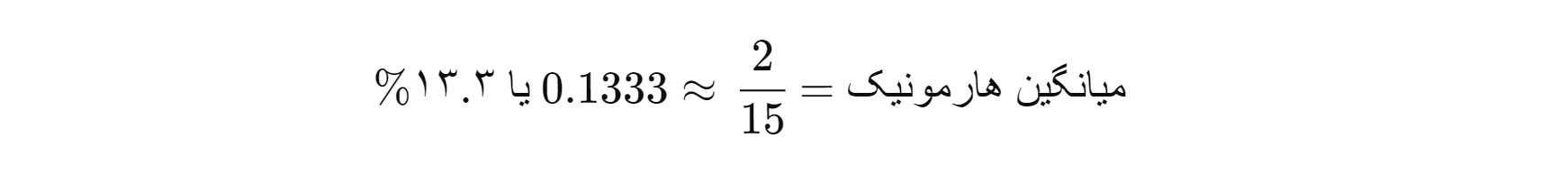
این نشان می‌دهد که میانگیـن هارمونیک نرخ بهره تقریباً ۱۳.۳% است.

چرا میانگین ها برای سرمایه گذاران حائز اهمیت اند؟

میانگین یک شاخص آماری است که برای سنجش عملکرد در طول زمان استفاده می‌شود. در زمینه سرمایه‌گذاری، میانگیـن برای درک عملکرد قیمت سهام یک شرکت در طول روزها، ماه‌ها یا سال‌ها به کار می‌رود. در دنیای کسب‌وکار و سرمایه‌گذاری، میانگیـن به طور گسترده برای موارد زیر استفاده می‌شود:

• میتوان تعیین کرد که آیا ارزش یک سهام در بالاتر یا پایین‌تر از میانگیـن خود در یک دوره زمانی مشخص معامله می‌شود.
• مقایسه نرخ بازده متوسط بازارهای گسترده در دوران رکودهای قبلی یا دوره‌های تورمی برای هدایت تصمیم‌گیری.
• میتوان بررسی کرد که آیا حجم معاملات یا تعداد سفارشات بازار با فعالیت بازار همخوانی دارد.
• میتوانید عملکرد عملیاتی یک شرکت را تحلیل کنید. برخی از نسبت‌های مالی مانند نسبت «روزهای فروش معوق» نیاز به تعیین میانگیـن مانده حساب‌های دریافتنی برای صورت کسر دارند.
• میتوانید داده‌های کلان اقتصادی مانند میانگیـن نرخ بیکاری را در طول زمان کمّی کنید تا سلامت کلی اقتصاد را تعیین کنید.

تفاوت میانگین، میانه و مد چیست؟

میانگیـن به مقدار متوسط یک مجموعه داده اشاره دارد. میانه نقطه‌ای است که 50 درصد داده‌ها در بالاتر یا پایین‌تر از آن قرار دارند. مد نیز به مقداری گفته می‌شود که بیشترین تکرار را در میان داده‌ها دارد. با رسم توزیع داده‌ها می‌توان به‌طور بصری میانگیـن را مشاهده کرد. در یک توزیع نرمال، میانگیـن، میانه و مد همه یکسان بوده و در مرکز نمودار قرار می‌گیرند.

نکات کلیدی میانگین ها در اقتصاد

• میانگیـن، مقدار متوسط ریاضی یک مجموعه از دو یا چند عدد است.
• میانگیـن حسابی و میانگیـن هندسی دو نوع میانگین هستند.
• برای پیدا کردن میانگیـن حسابی، اعداد یک مجموعه را با هم جمع کرده و بر تعداد اعداد موجود در مجموعه تقسیم می‌کنیم.
• برای محاسبه میانگیـن هندسی، همه مقادیر موجود در یک مجموعه داده را در هم ضرب کرده و سپس ریشه‌ی حاصل‌ضرب را به اندازه تعداد مقادیر موجود در آن مجموعه محاسبه می‌کنیم.

نتیجه گیری

میانگین ها در اقتصاد ابزارهای مهم و مفیدی هستند که به تحلیل داده‌ها و اتخاذ تصمیمات کمک می‌کنند. اما باید به چالش‌های مرتبط با آن‌ها نیز توجه کنیم و از معیارهای آماری دیگر استفاده کنیم تا واقعیت‌های اقتصادی را بهتر درک کنیم. استفاده صحیح از میانگیـن ها می‌تواند به سیاست‌گذاران و محققان کمک کند تا به نتایج دقیق‌تری دست یابند و سیاست‌های مؤثرتری برای بهبود وضعیت اقتصادی طراحی کنند.

در نهایت، برای افزایش کارایی تصمیم‌گیری‌های اقتصادی، ضروری است که میانگیـن ها به عنوان یکی از ابزارهای تحلیلی در کنار سایر روش‌ها و ابزارهای آماری به کار گرفته شوند تا تصویر جامع‌تری از وضعیت اقتصادی به دست آید.