مدل دوجملهای چیست؟
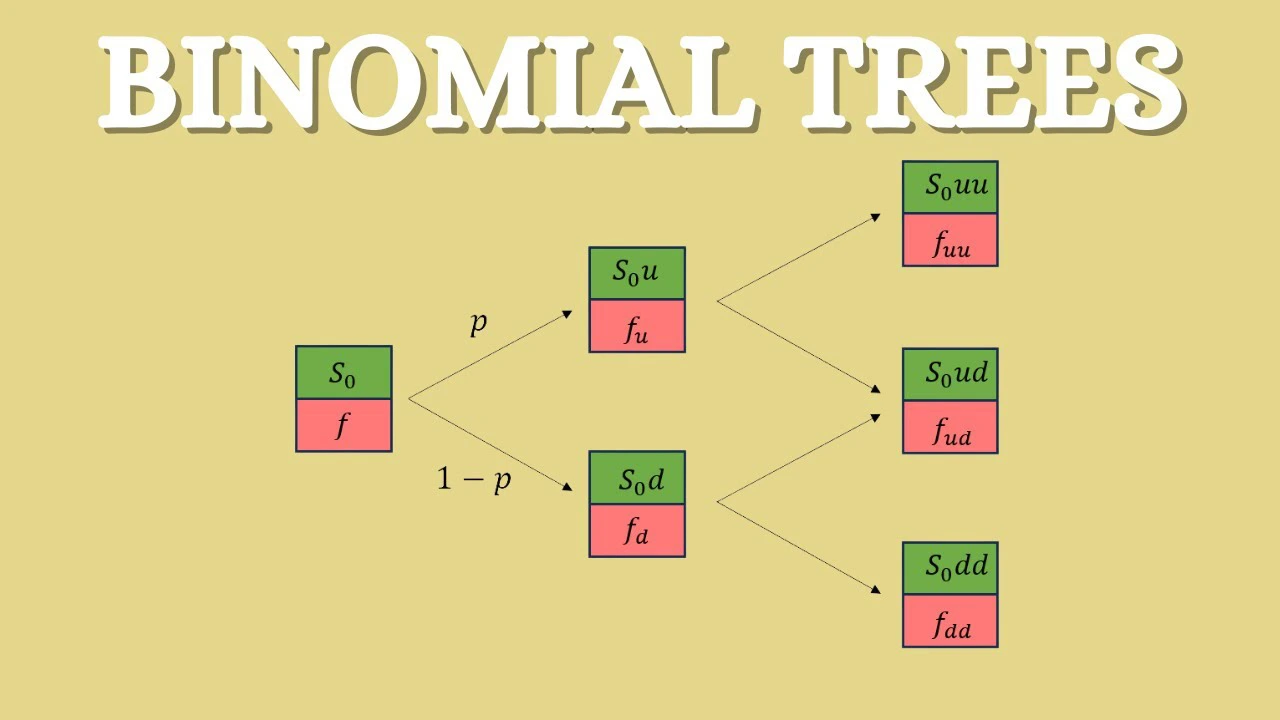
مدل دوجملهای Binomial Model
مدل دوجملهای (Binomial Model) یک روش عددی در ریاضیات مالی است که برای قیمتگذاری اختیار معاملهها (Options) و سایر مشتقات مالی به کار میرود. این مدل برای اولین بار توسط جان کاکس، استیون راس و مارک روبینشتاین در سال ۱۹۷۹ معرفی شد. هدف آن، ارائه یک ابزار ساده و انعطافپذیر برای تعیین ارزش ابزارهای مشتقه، در بازاری است که در آن قیمت داراییها با گذر زمان تغییر میکند.
برخلاف مدل بلک-شولز که از فرمولهای بسته تحلیلی استفاده میکند، مدل دوجملهای از ساختار گسسته و رویکرد درختی بهره میبرد و میتواند در فواصل زمانی مشخص، سناریوهای مختلف را بررسی کند.
دوره جامع معاملات آپشن، راهی ساده برای درآمد دلاری در اوقات فراغت | همین حالا کلیک کن.
تاریخچه مدل دوجملهای
قبل از توسعه مدل دوجملهای، قیمتگذاری اختیار معاملهها عمدتاً با استفاده از مدل بلک-شولز انجام میشد که در سال ۱۹۷۳ معرفی شده بود. با این حال، مدل بلک-شولز محدودیتهایی داشت، از جمله عدم توانایی در قیمتگذاری دقیق اختیار معاملههای آمریکایی که میتوانند قبل از سررسید اجرا شوند. همچنین، مدل بلک-شولز بر مفروضات پیچیدهای مانند تغییرات پیوسته قیمت و توزیع لگاریتمی نرمال وابسته بود که درک و پیادهسازی آن برای برخی از معاملهگران دشوار بود.
در اواخر دهه ۱۹۷۰، جان کاکس، استفان راس و مارک روبینشتاین با هدف ارائه روشی سادهتر و انعطافپذیرتر برای قیمتگذاری اختیار معاملهها، مدل دوجملهای را توسعه دادند. مقاله آنها در سال ۱۹۷۹ در مجله Journal of Financial Economics با عنوان “Option Pricing: A Simplified Approach” منتشر شد و به سرعت مورد توجه قرار گرفت. این مدل به دلیل شهودی بودن و امکان استفاده در سناریوهای پیچیدهتر، به یکی از ابزارهای استاندارد در تحلیل مالی تبدیل شد.
تأثیرات اولیه
مدل دوجملهای به دلیل سهولت محاسباتی و قابلیت مدلسازی سناریوهای مختلف، بهویژه در بازارهای مشتقه، به سرعت در میان معاملهگران و تحلیلگران مالی محبوب شد. این مدل همچنین به عنوان پایهای برای توسعه روشهای عددی پیشرفتهتر، مانند روشهای مونتکارلو و تفاوت محدود (Finite Difference Methods)، مورد استفاده قرار گرفت.
هدف اصلی مدل دوجملهای
مانند مدل بلک-شولز، هدف اصلی مدل دوجملهای نیز محاسبه قیمت نظری (Theoretical Price) یا ارزش منصفانه (Fair Value) قراردادهای اختیار معامله است. با این تفاوت که مدل دوجملهای به دلیل ساختار گسسته خود، برای قیمتگذاری اختیار معامله آمریکایی (American Options) که میتوانند در هر زمانی قبل از تاریخ سررسید اعمال شوند، بسیار مناسبتر است. این در حالی است که مدل بلک-شولز اساساً برای اختیارات اروپایی طراحی شده است.
ایده اصلی مدل دوجملهای
ایدهی پایه مدل دوجملهای بسیار ساده اما قدرتمند است:
فرض کنید قیمت یک دارایی (مثلاً سهام) در هر بازه زمانی کوتاه فقط میتواند دو حالت داشته باشد:
- افزایش یابد (Up)
- کاهش یابد (Down)
با ادامه این فرآیند برای چند دوره متوالی، میتوان یک درخت دوجملهای (Binomial Tree) ساخت که در آن، تمام مسیرهای ممکن قیمتگذاری دارایی رسم شده است. در گرههای انتهایی درخت (زمان سررسید)، ارزش اختیار محاسبه میشود و سپس با استفاده از تنزیل به عقب (Backward Induction)، ارزش اختیار در زمان حال به دست میآید.
دوره جامع معاملات آپشن، راهی ساده برای درآمد دلاری در اوقات فراغت | همین حالا کلیک کن.
اجزای اصلی مدل دوجملهای
برای ساختن مدل دوجملهای، به پارامترهای زیر نیاز داریم:
۱. قیمت اولیه دارایی پایه (S)
قیمتی که دارایی در زمان آغاز مدل دارد.
۲. درصد رشد (u) و درصد کاهش (d) در هر مرحله
بهصورت ساده:
- u=eσΔtu = e^{\sigma \sqrt{\Delta t}}u=eσΔt
- d=1ud = \frac{1}{u}d=u1
که در آن σ\sigmaσ نوسانپذیری سالانه دارایی و Δt\Delta tΔt مدتزمان هر مرحله (به سال) است.
۳. نرخ بهره بدون ریسک (r)
که برای تنزیل ارزش آینده به زمان حال استفاده میشود.
۴. احتمال ریسکخنثی (Risk-Neutral Probability)
برای بیطرفسازی از ریسک در محاسبه ارزش اختیار. این احتمال به شکل زیر تعریف میشود:
p=erΔt−du−dp = \frac{e^{r \Delta t} – d}{u – d}p=u−derΔt−d
که در آن:
- ppp: احتمال افزایش قیمت تحت فرض ریسکخنثی
- 1−p1-p1−p: احتمال کاهش قیمت
کاربردهای مدل دوجملهای
مدل دوجملهای به دلیل انعطافپذیری و سادگی در حوزههای مختلف مالی کاربرد دارد:
- قیمتگذاری اختیار معاملههای آمریکایی: این مدل به دلیل توانایی در نظر گرفتن اجرای زودهنگام، برای قیمتگذاری اختیار معاملههای آمریکایی بسیار مناسب است.
- ارزشگذاری ابزارهای مشتقه پیچیده: مدل دوجملهای میتواند برای قیمتگذاری ابزارهای مشتقه عجیبوغریب (Exotic Options) مانند اختیار معاملههای آسیایی یا مانعدار (Barrier Options) استفاده شود.
- مدیریت ریسک: این مدل به معاملهگران امکان میدهد تا استراتژیهای پوشش ریسک (Hedging) را با استفاده از نسبتهای حساسیت (Greeks) طراحی کنند.
- تحلیل سناریوها: درخت دوجملهای امکان بررسی سناریوهای مختلف بازار را فراهم میکند.
- آموزش و پژوهش: به دلیل شهودی بودن، این مدل در آموزش مالی و تحقیقات دانشگاهی کاربرد گستردهای دارد.
مفروضات مدل دوجملهای
مدل دوجملهای بر مجموعهای از مفروضات سادهساز استوار است که برخی از آنها با مدل بلک-شولز مشترک هستند:
- تغییرات گسسته قیمت: قیمت دارایی پایه (مانند سهام) در هر بازه زمانی فقط میتواند به دو حالت افزایش یا کاهش یابد (حالت دوجملهای).
- جهان بدون ریسک: در یک جهان بدون ریسک، بازده مورد انتظار دارایی برابر با نرخ بهره بدون ریسک است.
- نرخ بهره بدون ریسک ثابت: نرخ بهره بدون ریسک (Risk-Free Rate) در طول دوره قرارداد ثابت است.
- بازار بدون اصطکاک: فرض میشود که هیچ هزینه معاملاتی، مالیاتی یا محدودیت در خرید و فروش وجود ندارد.
- نوسانات مشخص: نوسانات قیمت دارایی پایه (Volatility) در طول زمان مشخص و قابل تخمین است.
- عدم پرداخت سود نقدی: در نسخه پایه مدل، فرض میشود که دارایی پایه سود نقدی پرداخت نمیکند (هرچند نسخههای اصلاحشده این مورد را در نظر میگیرند).
این مفروضات امکان مدلسازی تغییرات قیمت را به صورت یک درخت دوجملهای (Binomial Tree) فراهم میکنند که پایه محاسبات مدل است.
مفهوم و اساس مدل دوجملهای
مدل دوجملهای بر پایه یک فرض ساده اما قدرتمند بنا شده است: در هر گام زمانی، قیمت دارایی پایه (مثلاً یک سهام) فقط میتواند دو حالت داشته باشد: یا افزایش (Up) پیدا کند یا کاهش (Down) یابد. این دو حالت، که به “گامهای دوجملهای” معروفاند، پایه و اساس ساختار درختی مدل را تشکیل میدهند.
مدل با ساخت یک “درخت دوجملهای” (Binomial Tree) آغاز میشود. این درخت نموداری است که مسیرهای احتمالی قیمت دارایی پایه را از زمان حال تا تاریخ سررسید اختیار معامله نشان میدهد. هر “گره” (Node) در درخت نشاندهنده یک قیمت احتمالی برای دارایی پایه در یک نقطه زمانی خاص است.
اصول کلیدی مدل دوجملهای:
- عدم آربیتراژ (No-Arbitrage): همانند بلک-شولز، مدل دوجملهای نیز بر این فرض استوار است که در بازار فرصت آربیتراژ (کسب سود بدون ریسک) وجود ندارد. این اصل اساسی برای تعیین قیمت منصفانه اختیار معامله ضروری است.
- خلق پرتفوی بدون ریسک (Risk-Free Portfolio): ایده اصلی این است که میتوان با ترکیب دارایی پایه (سهام) و اختیار معامله به نسبتی مشخص، یک پرتفوی “پوششدادهشده” (Hedged Portfolio) ایجاد کرد که در هر دو حالت افزایش یا کاهش قیمت دارایی پایه، ارزش یکسانی داشته باشد. این پرتفوی بدون ریسک، باید بازدهی برابر با نرخ بهره بدون ریسک داشته باشد.
- احتمالات خنثی نسبت به ریسک (Risk-Neutral Probabilities): در مدل دوجملهای، قیمتگذاری با استفاده از احتمالات خنثی نسبت به ریسک انجام میشود. این احتمالات، بر اساس این فرض محاسبه میشوند که سرمایهگذاران نسبت به ریسک خنثی هستند و تنها به امید ریاضی بازدهی اهمیت میدهند. در این دنیای فرضی، انتظار بازدهی هر دارایی برابر با نرخ بهره بدون ریسک است.
دوره جامع معاملات آپشن، راهی ساده برای درآمد دلاری در اوقات فراغت | همین حالا کلیک کن.
چگونه از مدل دوجملهای استفاده کنیم؟
این مدل برای ابزارهای مالی مختلف از جمله اختیارهای استاندارد آمریکایی و اروپایی، مشتقات پیچیده، و گزینههای واقعی (real options) در مالی شرکتی کاربرد دارد. همچنین برای تحلیل ریسک، تصمیمگیری استراتژیک و طراحی پوشش ریسک (hedging) استفاده میشود.
مؤسسات مالی از این مدل برای برآورد ریسک نگهداری اختیار استفاده میکنند. با شبیهسازی بازار و بررسی تأثیر تغییرات نرخ بهره و قیمت سهام، مدیران ریسک میتوانند برای شرایط مختلف آماده شوند.
معاملهگران از این مدل برای تدوین استراتژیهای هج مثل هج دلتا (Delta Hedging) استفاده میکنند.
نکته: اختیارهای آمریکایی میتوانند در هر لحظه قبل از تاریخ انقضا اعمال شوند؛ اما اختیارهای اروپایی فقط در تاریخ انقضا قابل اعمال هستند.
علاوه بر بازارهای مالی، از مدل دوجملهای برای تحلیل گزینههای واقعی در تصمیمگیریهای سرمایهگذاری نیز استفاده میشود؛ مثل توسعه، توقف یا به تعویق انداختن یک پروژه.
همچنین بهعنوان ابزار آموزشی عالی بهکار میرود و به درک اصول قیمتگذاری اختیار کمک میکند.
شرکتها نیز از این مدل برای قیمتگذاری اوراق قرضه قابل تبدیل، وارانها (Warrants) و اختیارهای سهام کارکنان استفاده میکنند.
روش محاسباتی مدل دوجملهای
مدل دوجملهای با استفاده از یک درخت دوجملهای (Binomial Tree) قیمت اختیار معامله را محاسبه میکند. این درخت تغییرات ممکن در قیمت دارایی پایه را در طول زمان مدلسازی میکند. مراحل کلی محاسبات به شرح زیر است:
1. ساخت درخت دوجملهای
زمان تا سررسید قرارداد ((T)) به (n) بازه زمانی کوچک تقسیم میشود.
در هر بازه زمانی، قیمت دارایی پایه ((S_0)) میتواند با ضریب (u) (افزایش) یا (d) (کاهش) تغییر کند.
ضرایب (u) و (d) به صورت زیر تعریف میشوند: [ u = e^{\sigma \sqrt{\Delta t}} ] [ d = e^{-\sigma \sqrt{\Delta t}} = \frac{1}{u} ] که در آن (\sigma) نوسانات سالانه دارایی و (\Delta t = T/n) طول هر بازه زمانی است.
قیمت دارایی در هر گره از درخت به صورت (S_0 u^i d^{n-i}) محاسبه میشود، که (i) تعداد حرکتهای صعودی است.
2. محاسبه احتمال بدون ریسک
در یک جهان بدون ریسک، احتمال حرکت صعودی ((p)) و نزولی ((1-p)) به صورت زیر محاسبه میشود: [ p = \frac{e^{r \Delta t} – d}{u – d} ] که (r) نرخ بهره بدون ریسک است.
3. محاسبه ارزش اختیار معامله در سررسید
برای یک اختیار خرید (Call Option)، ارزش در زمان سررسید برابر است با: [ C = \max(S_T – K, 0) ]
برای یک اختیار فروش (Put Option): [ P = \max(K – S_T, 0) ] که (S_T) قیمت دارایی در زمان سررسید و (K) قیمت توافقی است.
4. محاسبه ارزش به عقب (Backward Induction)
از گرههای پایانی درخت (در زمان سررسید) شروع کرده و به سمت عقب حرکت میکنیم.
در هر گره، ارزش اختیار معامله به صورت زیر محاسبه میشود: [ V = e^{-r \Delta t} [p V_u + (1-p) V_d] ] که (V_u) و (V_d) ارزشهای اختیار معامله در گرههای صعودی و نزولی بعدی هستند.
برای اختیار معاملههای آمریکایی، در هر گره بررسی میشود که آیا اجرای زودهنگام (Early Exercise) سودآورتر است یا خیر: [ V = \max(\text{ارزش ذاتی}, e^{-r \Delta t} [p V_u + (1-p) V_d]) ]
5. نتیجه نهایی
با ادامه محاسبات به عقب تا گره ابتدایی (زمان حال)، قیمت منصفانه اختیار معامله محاسبه میشود.
مثال ساده
فرض کنید قیمت فعلی سهام ((S_0)) ۱۰۰ دلار، قیمت توافقی ((K)) ۱۰۰ دلار، زمان تا سررسید ((T)) ۱ سال، نرخ بهره بدون ریسک ((r)) ۵٪، نوسانات ((\sigma)) ۲۰٪ و تعداد بازههای زمانی ((n)) ۲ باشد.
-
محاسبه (u) و (d): [ u = e^{0.2 \sqrt{0.5}} \approx 1.1519, \quad d = \frac{1}{u} \approx 0.8681 ]
-
محاسبه احتمال بدون ریسک ((p)): [ p = \frac{e^{0.05 \times 0.5} – 0.8681}{1.1519 – 0.8681} \approx 0.5534 ]
-
ساخت درخت قیمت سهام:
-
گره ابتدایی: (S_0 = 100)
-
گرههای بازه اول: (100 \times 1.1519 = 115.19)، (100 \times 0.8681 = 86.81)
-
گرههای بازه دوم: (115.19 \times 1.1519 = 132.76)، (115.19 \times 0.8681 = 100.00)، (86.81 \times 0.8681 = 75.35)
-
-
محاسبه ارزش اختیار خرید در سررسید:
-
گره (132.76): (\max(132.76 – 100, 0) = 32.76)
-
گره (100.00): (\max(100 – 100, 0) = 0)
-
گره (75.35): (\max(75.35 – 100, 0) = 0)
-
-
محاسبه به عقب برای گرههای میانی و ابتدایی:
-
این فرآیند ادامه مییابد تا قیمت اختیار معامله در زمان حال محاسبه شود.
-
مثال دنیای واقعی از مدل دوجملهای
فرض کنید قیمت سهامی در حال حاضر ۱۰۰ دلار است و در یک ماه آینده یا به ۱۱۰ دلار یا به ۹۰ دلار میرسد. یک اختیار خرید (Call) با قیمت اعمال ۱۰۰ دلار و سررسید یکماهه در نظر بگیرید.
- در حالت افزایش: ارزش اختیار = ۱۰ دلار
- در حالت کاهش: ارزش اختیار = ۰ دلار
حال فرض کنید سرمایهگذار نیمی از یک سهم را میخرد و یک اختیار خرید میفروشد.
- هزینه امروز = ۵۰ دلار – قیمت اختیار
- ارزش پرتفوی در حالت افزایش = ۵۵ – max(۱۱۰ – ۱۰۰, ۰) = ۴۵
- ارزش پرتفوی در حالت کاهش = ۴۵ – max(۹۰ – ۱۰۰, ۰) = ۴۵
چون در هر حالت ارزش پرتفوی یکسان است، نرخ بازدهی باید معادل نرخ بدون ریسک باشد (بدون آربیتراژ). این پایهی محاسبات قیمت اختیار در مدل دوجملهای است.
نکته: این مدل پایهای برای مدلهای مشبک (Lattice Models) پیچیدهتر در مهندسی مالی مدرن است.
مزایای مدل دوجملهای
- شهودی و بصری: ساختار درختی آن، فهم فرآیند قیمتگذاری را بسیار آسانتر از مدل بلک-شولز میکند.
- مناسب برای اختیارات آمریکایی: توانایی مدل برای در نظر گرفتن امکان اعمال زودهنگام (Early Exercise) آن را برای قیمتگذاری اختیارات آمریکایی بسیار مناسب میسازد.
- انعطافپذیری: میتوان آن را برای قیمتگذاری اختیارات با ویژگیهای پیچیدهتر (مانند اختیارات با موانع – Barrier Options، اختیارات با مسیر وابسته – Path-Dependent Options) تطبیق داد.
- بدون نیاز به فرمولهای پیچیده ریاضی: محاسبات آن عمدتاً بر پایه ضرب، جمع و لگاریتم ساده است و نیاز به درک عمیق از حساب دیفرانسیل و انتگرال تصادفی ندارد.
- همگرایی به مدل بلک-شولز: با افزایش تعداد گامها (N) تا بینهایت، مدل دوجملهای به نتایج مدل بلک-شولز همگرا میشود. این نشاندهنده ارتباط عمیق بین دو مدل است.
معایب مدل دوجملهای
با وجود مزایای زیاد، مدل دوجملهای محدودیتهایی نیز دارد:
- پیچیدگی محاسباتی: با افزایش تعداد بازههای زمانی ((n))، تعداد گرههای درخت به صورت تصاعدی افزایش مییابد که محاسبات را زمانبر میکند.
- فرض تغییرات گسسته: مدل فرض میکند که قیمت دارایی فقط میتواند به دو حالت تغییر کند، در حالی که در واقعیت تغییرات قیمت پیوسته و پیچیدهتر هستند.
- نوسانات ثابت: مانند مدل بلک-شولز، این مدل فرض میکند که نوسانات ثابت است، در حالی که در بازارهای واقعی نوسانات پویا هستند.
- وابستگی به انتخاب پارامترها: دقت مدل به انتخاب صحیح پارامترهای (u)، (d) و (p) وابسته است.
- عدم پشتیبانی از پرشهای ناگهانی: این مدل نمیتواند پرشهای ناگهانی در قیمت داراییها (مانند اخبار مهم بازار) را به خوبی مدلسازی کند.
مدل دوجملهای و اختیارهای آمریکایی
یکی از بزرگترین مزایای مدل دوجملهای، توانایی آن در قیمتگذاری اختیارهای آمریکایی است. در هر گره از درخت، مدل بررسی میکند که آیا اجرای اختیار در آن نقطه بهصرفه است یا خیر (مفهوم «اعمال زودهنگام»). این ویژگی در مدل بلک-شولز وجود ندارد.
دوره جامع معاملات آپشن، راهی ساده برای درآمد دلاری در اوقات فراغت | همین حالا کلیک کن.
نسخههای اصلاحشده و پیشرفتها
برای رفع محدودیتهای مدل دوجملهای، نسخههای اصلاحشدهای توسعه یافتهاند:
- مدل سهجملهای (Trinomial Model): به جای دو حالت (صعودی و نزولی)، یک حالت میانی نیز در نظر گرفته میشود که دقت مدل را افزایش میدهد.
- مدلهای تطبیقی: این مدلها از روشهای عددی پیشرفتهتر مانند روشهای مونتکارلو برای بهبود دقت استفاده میکنند.
- مدلهای نوسانات تصادفی: برای در نظر گرفتن تغییرات پویای نوسانات، مدلهای پیشرفتهتری توسعه شدهاند.
- مدلهای پرش-انتشار: این مدلها پرشهای ناگهانی در قیمت داراییها را به مدل اضافه میکنند.
نکات کلیدی
- مدل قیمتگذاری اختیارات دوجملهای (Binomial Option Pricing Model) تکنیکی برای ارزشگذاری اختیار معامله (Option) است که با شبیهسازی مسیرهای ممکن برای قیمت دارایی پایه در طول عمر اختیار، عمل میکند.
- این مدل فرض میکند که قیمت دارایی پایه در هر بازه زمانی فقط میتواند به میزان مشخصی افزایش یا کاهش یابد؛ این موضوع به ساختار “درخت دوجملهای” (binomial tree) از حرکتهای احتمالی قیمت منجر میشود.
- این مدل برای ارزشگذاری اختیارهای سبک آمریکایی (American-style options) بسیار مفید است؛ زیرا این اختیارها میتوانند در هر زمان قبل از سررسید اعمال شوند. مدل دوجملهای امکان تحلیل بهترین زمان برای اعمال را فراهم میکند.
- با افزایش تعداد مراحل زمانی، دقت مدل بالا میرود و در نهایت، با مدل بلک-شولز (Black-Scholes) همگرا میشود.
- ورودیهای کلیدی این مدل عبارتاند از: قیمت سهام، قیمت اعمال (Strike Price)، زمان باقیمانده تا سررسید، نرخ بهره بدون ریسک، و نوسانپذیری دارایی.
- این مدل با استفاده از یک درخت گسسته مرحلهای (Stepwise Binary Tree) قیمتهای ممکن اختیار را در طول زمان تخمین میزند و امکان تحلیل اختیارهای قابلاعمال در هر لحظه را فراهم میکند.
رابطه مدل دوجملهای با مدل بلک-شولز
اگر تعداد مراحل مدل دوجملهای را بسیار زیاد کنیم و طول هر مرحله را بسیار کوچک بگیریم، خروجی نهایی بهسمت قیمت حاصل از مدل بلک-شولز میل میکند. در واقع، میتوان گفت مدل دوجملهای تقریب عددی مدل بلک-شولز است.
مقایسه مدل دوجملهای با مدل بلک-شولز
|
ویژگی |
مدل دوجملهای |
مدل بلک-شولز |
|---|---|---|
|
نوع اختیار معامله |
مناسب برای آمریکایی و اروپایی |
فقط برای اروپایی |
|
تغییرات قیمت |
گسسته (درخت دوجملهای) |
پیوسته (توزیع لگاریتمی نرمال) |
|
پیچیدگی محاسباتی |
با افزایش بازهها پیچیدهتر میشود |
محاسبات سادهتر با فرمول بسته |
|
انعطافپذیری |
انعطافپذیر برای ابزارهای پیچیده |
محدود به اختیار معاملههای ساده |
|
درک شهودی |
ساده و شهودی |
پیچیدهتر به دلیل معادلات دیفرانسیل |
مدل دوجملهای به دلیل انعطافپذیری در مدلسازی اجرای زودهنگام و ابزارهای پیچیده، در بسیاری از موارد به مدل بلک-شولز ترجیح داده میشود. با این حال، برای اختیار معاملههای اروپایی ساده، مدل بلک-شولز به دلیل سرعت محاسباتی و سادگی ترجیح داده میشود.
جمعبندی
مدل دوجملهای یکی از پایهایترین و درعینحال انعطافپذیرترین مدلها در ریاضیات مالی است. این مدل با سادهسازی رفتار قیمت داراییها به دو حرکت «بالا» یا «پایین» در هر مرحله زمانی، امکان تحلیل و قیمتگذاری دقیق ابزارهای مشتقه را فراهم میکند. توانایی آن در درک ساختار زمانی قیمت، اعمال زودهنگام و نیز سازگاری با ویژگیهای متنوع بازار، آن را به یکی از مهمترین ابزارهای تحلیلی در حوزه اختیار معامله تبدیل کرده است.
سوالات متداول
۱. مدل دوجملهای چیست و چه کاربردی دارد؟
مدل دوجملهای یک روش عددی برای قیمتگذاری اختیار معامله و سایر مشتقات مالی است. این مدل با فرض دو حالت ممکن برای قیمت دارایی در هر بازه زمانی (بالا یا پایین رفتن قیمت)، یک درخت احتمالاتی میسازد و با تحلیل معکوس، ارزش اختیار را محاسبه میکند.
۲. چرا به آن مدل «دوجملهای» میگویند؟
زیرا در هر مرحله زمانی فقط دو حالت برای تغییر قیمت دارایی در نظر گرفته میشود: رشد (up) یا کاهش (down). به همین دلیل، مدل دارای ساختار دوجملهای یا دو شاخهای است.
۳. تفاوت مدل دوجملهای با مدل بلک-شولز چیست؟
- مدل دوجملهای گسسته است، ولی بلک-شولز پیوسته.
- مدل دوجملهای برای اختیارهای آمریکایی قابل استفاده است، بلک-شولز تنها برای اختیارهای اروپایی مناسب است.
- مدل دوجملهای سادهتر قابل پیادهسازی عددی است، اما نیازمند مراحل بیشتر برای دقت بالاست.
۴. آیا مدل دوجملهای فقط برای اختیارهای اروپایی کاربرد دارد؟
خیر، برتری اصلی مدل دوجملهای در این است که میتواند برای اختیارهای آمریکایی نیز به کار رود، چون اجازه بررسی اعمال زودهنگام را در هر گره از درخت دارد.
۵. مدل دوجملهای برای چه نوع داراییهایی مناسب است؟
برای داراییهایی که نوسانپذیری دارند (مانند سهام، ارز، کالاها) و اختیارهای مرتبط با آنها. همچنین میتواند برای داراییهایی که سود نقدی پرداخت میکنند یا نرخ بهره متغیر دارند نیز تنظیم شود.
۶. آیا افزایش تعداد مراحل در مدل دوجملهای دقت را بالا میبرد؟
بله. هرچه تعداد مراحل زمانی بیشتر باشد، مدل دقیقتر خواهد بود و نتایج آن بیشتر به مدلهای پیوسته مانند بلک-شولز نزدیک میشود. اما افزایش مراحل باعث رشد حجم محاسبات میشود.
۷. آیا مدل دوجملهای تنها راه برای قیمتگذاری اختیار معامله است؟
خیر. روشهای دیگری نیز وجود دارند مانند:
- مدل بلک-شولز
- روش مونتکارلو
- حل عددی معادله دیفرانسیل پارهای (PDE)
اما مدل دوجملهای یکی از سادهترین و پایهایترین روشهاست که هنوز هم بسیار کاربرد دارد.
۸. چه فرضیاتی در مدل دوجملهای وجود دارد؟
- بازار بدون آربیتراژ است.
- امکان قرضگیری و سرمایهگذاری با نرخ بهره بدون ریسک وجود دارد.
- تغییرات قیمت فقط در قالب بالا یا پایین ممکن است.
- قیمتها از یک فرآیند تصادفی پیروی میکنند.
- احتمالها در چارچوب ریسکخنثی تعریف میشوند.
۹. چطور میتوان با استفاده از مدل دوجملهای، اختیار معامله را قیمتگذاری کرد؟
با مراحل زیر:
- محاسبه مقدار u و d (افزایش و کاهش قیمت در هر مرحله)
- ساخت درخت قیمت دارایی پایه
- محاسبه ارزش اختیار در زمان سررسید
- حرکت معکوس و محاسبه ارزش در هر گره
- رسیدن به ارزش نهایی در زمان حال
۱۰. آیا نرمافزار یا ابزار خاصی برای پیادهسازی مدل دوجملهای وجود دارد؟
بله. این مدل به سادگی در نرمافزارهایی مانند Excel، Python، MATLAB یا R قابل پیادهسازی است. حتی ماشینحسابهای مالی حرفهای هم امکان اجرای آن را دارند.
پست های مرتبط

1404/11/12

1404/10/16

1404/10/11






دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.