ضریب تورم واریانس (VIF) چیست؟

ضریب تورم واریانس (VIF) Variance Inflation Factor
ضریب تورم واریانس (VIF) شدت چند خطی بودن را در تحلیل رگرسیون اندازه گیری می کند . این یک مفهوم آماری است که نشان دهنده افزایش واریانس یک ضریب رگرسیون در نتیجه همخطی بودن است.
به طور خلاصه:
- عامل تورم واریانس (VIF) برای تشخیص شدت چند خطی در تحلیل رگرسیون حداقل مربعات معمولی (OLS) استفاده میشود.
- چند خطی بودن واریانس و خطای نوع II را افزایش می دهد. ضریب یک متغیر را ثابت اما غیر قابل اعتماد می کند.
- VIF تعداد واریانس های متورم ناشی از چند خطی را اندازه گیری می کند.
درک یک عامل تورم واریانس (VIF)
عامل تورم واریانس ابزاری برای کمک به شناسایی درجه چند خطی بودن است. رگرسیون چندگانه زمانی استفاده می شود که فردی بخواهد تأثیر متغیرهای متعدد را بر یک نتیجه خاص آزمایش کند. متغیر وابسته نتیجهای است که توسط متغیرهای مستقل – ورودیهای مدل – انجام میشود. چند خطی زمانی وجود دارد که یک رابطه خطی یا همبستگی بین یک یا چند متغیر یا ورودی مستقل وجود داشته باشد.
عامل تورم واریانس و چند خطی
در تحلیل رگرسیون حداقل مربعات معمولی (OLS)، چند خطی زمانی وجود دارد که دو یا چند متغیر مستقل رابطه خطی بین آنها را نشان دهند. به عنوان مثال، برای تجزیه و تحلیل رابطه اندازه شرکت و درآمد با قیمت سهام در یک مدل رگرسیونی، ارزش بازار و درآمد متغیرهای مستقل هستند.
ارزش بازار یک شرکت و کل درآمد آن رابطه قوی دارد. همانطور که یک شرکت درآمد فزاینده ای کسب می کند، اندازه آن نیز افزایش می یابد. این منجر به یک مشکل چند خطی در تحلیل رگرسیون OLS می شود. اگر متغیرهای مستقل در یک مدل رگرسیونی یک رابطه خطی کاملاً قابل پیش بینی را نشان دهند، به آن چند خطی کامل می گویند.
با چند خطی بودن، ضرایب رگرسیون هنوز ثابت هستند اما دیگر قابل اعتماد نیستند زیرا خطاهای استاندارد متورم هستند. به این معنی که قدرت پیش بینی مدل کاهش نمی یابد، اما ممکن است ضرایب با خطای نوع II از نظر آماری معنی دار نباشند.
بنابراین، اگر ضرایب متغیرها به صورت جداگانه معنی دار نباشند – به ترتیب در آزمون t نمی توان آنها را رد کرد – اما می توانند به طور مشترک واریانس متغیر وابسته را با رد در آزمون F و ضریب تعیین بالا توضیح دهند (R 2 ) ، ممکن است چند خطی وجود داشته باشد. این یکی از روش های تشخیص چند خطی است.
VIF یکی دیگر از ابزارهای رایج مورد استفاده برای تشخیص وجود چند خطی در یک مدل رگرسیونی است. اندازه گیری می کند که واریانس (یا خطای استاندارد) ضریب رگرسیون تخمینی به دلیل همخطی بودن چقدر افزایش یافته است.
استفاده از ضریب تورم واریانس
VIF را می توان با فرمول زیر محاسبه کرد:
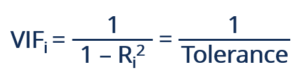
جایی که Ri 2 نشان دهنده ضریب تعیین تعدیل نشده برای رگرسیون i امین متغیر مستقل روی بقیه است. متقابل VIF به عنوان تحمل شناخته می شود . بسته به ترجیحات شخصی، می توان از VIF یا تلورانس برای تشخیص چند خطی استفاده کرد.
اگر Ri 2 برابر با ۰ باشد، واریانس متغیرهای مستقل باقیمانده را نمی توان از روی متغیر مستقل i پیش بینی کرد . بنابراین، زمانی که VIF یا تلورانس برابر با ۱ باشد، من متغییر مستقل با بقیه همبستگی ندارد، به این معنی که چند خطی در این مدل رگرسیونی وجود ندارد. در این حالت، واریانس ضریب رگرسیون یکم متورم نیست.
به طور کلی، یک VIF بالاتر از ۴ یا تحمل کمتر از ۰٫۲۵ نشان می دهد که ممکن است چند خطی وجود داشته باشد، و تحقیقات بیشتری مورد نیاز است. هنگامی که VIF بالاتر از ۱۰ یا تلرانس کمتر از ۰٫۱ باشد، چند خطی قابل توجهی وجود دارد که باید اصلاح شود.
با این حال، موقعیتهایی نیز وجود دارد که میتوان VFIهای بالا را با خیال راحت و بدون اینکه از چند خطی بودن رنج برد، نادیده گرفت. در زیر سه حالت از این قبیل وجود دارد:
- VIF های بالا فقط در متغیرهای کنترلی وجود دارد اما در متغیرهای مورد علاقه وجود ندارد. در این حالت متغیرهای مورد نظر با یکدیگر و یا متغیرهای کنترلی خطی نیستند. ضرایب رگرسیون تحت تاثیر قرار نمی گیرند.
- هنگامی که VIF های بالا در نتیجه گنجاندن محصولات یا قدرت های متغیرهای دیگر ایجاد می شوند، چند خطی بودن تأثیر منفی ایجاد نمی کند. به عنوان مثال، یک مدل رگرسیون هر دو x و x 2 را به عنوان متغیرهای مستقل خود شامل می شود.
- وقتی یک متغیر ساختگی که بیش از دو دسته را نشان میدهد دارای VIF بالایی باشد، لزوماً چند خطی وجود ندارد. اگر بخش کوچکی از موارد در دسته وجود داشته باشد، بدون توجه به اینکه آیا متغیرهای طبقهبندی با متغیرهای دیگر همبستگی دارند، متغیرها همیشه دارای VIF بالایی خواهند بود.
تصحیح چند خطی
از آنجایی که چند خطی بودن واریانس ضرایب را افزایش می دهد و باعث خطاهای نوع II می شود، تشخیص و اصلاح آن ضروری است. دو روش ساده و متداول برای تصحیح چند خطی وجود دارد که در زیر ذکر شده است:
- اولین مورد حذف یک (یا چند) از متغیرهای بسیار همبسته است. از آنجایی که اطلاعات ارائه شده توسط متغیرها زائد است، ضریب تعیین با حذف تا حد زیادی مختل نخواهد شد.
- روش دوم استفاده از تحلیل مؤلفه های اصلی (PCA) یا رگرسیون حداقل مربعات جزئی (PLS) به جای رگرسیون OLS است. رگرسیون PLS میتواند متغیرها را به مجموعهای کوچکتر و بدون همبستگی بین آنها کاهش دهد. در PCA، متغیرهای جدید ناهمبسته ایجاد می شوند. از دست دادن اطلاعات را به حداقل می رساند و قابلیت پیش بینی یک مدل را بهبود می بخشد.
پست های مرتبط

1404/11/12







دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.