استقرا معکوس (بازگشت به عقب) چیست؟

استقرا معکوس (بازگشت به عقب)

استقرا معکوس یا همان بازگشت به عقب (Backward Induction) یکی از روش‌های مهم و پرکاربرد در ریاضیات، منطق، علوم کامپیوتر و اقتصاد است. این روش به زبان ساده یعنی:
برای حل یک مسئله یا اثبات یک قضیه، به جای اینکه از ابتدا شروع کنیم، از انتهای مسئله یا از حالت پایانی شروع کرده و قدم به قدم به عقب برمی‌گردیم تا به حالت ابتدایی برسیم.

استقرا معکوس می‌گوید اگر بتوانیم:

1. وضعیت نهایی یک فرآیند را مشخص کنیم.
2. نشان دهیم که چگونه رسیدن به هر وضعیت قبلی به وضعیت بعدی منجر می‌شود.

آنگاه می‌توانیم به کمک بازگشت به عقب، تمام مراحل میانی و در نهایت نقطه آغاز را هم تحلیل کنیم.

به عبارت دیگر، استقرا معکوس روشی برای استدلال از انتها به ابتداست.

ویدئو آموزشی مرتبط با این مطلب

اصول پایه استقرا معکوس

شروع از پایان: تحلیل از آخرین مرحله یا حالت ممکن مسئله آغاز می‌شود.

تصمیم‌گیری بهینه: فرض بر این است که هر بازیکن یا عامل در هر مرحله بهترین تصمیم را با توجه به اطلاعات موجود می‌گیرد.

حرکت به عقب: پس از تعیین تصمیمات بهینه در مرحله نهایی، تحلیل‌گر به مرحله قبلی می‌رود و این فرآیند را تکرار می‌کند.

اطلاعات کامل: این روش معمولاً در موقعیت‌هایی استفاده می‌شود که بازیکنان از تمام اطلاعات مربوط به بازی آگاه هستند.

تاریخچه استقرا معکوس

مفهوم استقرا معکوس به‌طور رسمی در نظریه بازی‌ها در قرن بیستم توسط دانشمندانی مانند جان فون نویمان و اسکار مورگنسترن، که بنیان‌گذاران نظریه بازی‌ها بودند، توسعه یافت. بااین‌حال، ایده اصلی بازگشت به عقب در مسائل ریاضی و منطقی به قبل از شکل‌گیری رسمی نظریه بازی‌ها بازمی‌گردد. در دهه 1950، ریچارد بلمن (Richard Bellman) با معرفی برنامه‌ریزی پویا (Dynamic Programming) به تکامل این مفهوم کمک کرد. استقرا معکوس به‌عنوان یک ابزار محاسباتی برای حل مسائل چندمرحله‌ای در نظریه بازی‌ها و اقتصاد به‌کار گرفته شد و امروزه در زمینه‌های مختلفی از جمله هوش مصنوعی، علوم کامپیوتر، و مدیریت استفاده می‌شود.

ریشه و ارتباط با استقرا ریاضی

• در استقرا ریاضی معمولی، ما از یک حالت پایه (مثلاً (n=1)) شروع می‌کنیم و نشان می‌دهیم اگر گزاره برای (n=k) درست باشد، برای (n=k+1) هم درست خواهد بود. این یعنی حرکت از ابتدا به سمت جلو.
• در استقرا معکوس برعکس عمل می‌کنیم: از یک حالت پایانی یا بزرگ‌ترین مقدار شروع می‌کنیم و نشان می‌دهیم اگر برای (n=k) درست است، برای (n=k-1) هم درست خواهد بود.

به همین دلیل به آن استقرا رو به عقب می‌گویند.

کاربردهای استقرا معکوس

در ریاضیات

• اثبات گزاره‌ها در بازه‌های معکوس (مثلاً اثبات درستی فرمول‌ها از (n) به (n-1)).
• حل مسائل شمارشی و الگوریتمی.

در علوم کامپیوتر

• طراحی الگوریتم‌های بازگشتی.
• تحلیل Dynamic Programming (برنامه‌نویسی پویا) که بر پایه بازگشت به عقب است.
• حل مسائل بهینه‌سازی مثل کوتاه‌ترین مسیر یا کمترین هزینه.

در نظریه بازی‌ها و اقتصاد

• تحلیل بازی‌های ترتیبی (Sequential Games).
• انتخاب استراتژی‌های عقلانی در مذاکرات، مزایده‌ها یا رقابت‌ها.
• مثال مشهور: مسئله تقسیم کیک یا پول؛ افراد به عقب برمی‌گردند و پیش‌بینی می‌کنند اگر به مراحل پایانی برسند، طرف مقابل چه می‌کند. سپس بر اساس این پیش‌بینی‌ها در مرحله اول تصمیم می‌گیرند.

د) در منطق و فلسفه

• برای تحلیل گزاره‌هایی که از آینده به گذشته معنا پیدا می‌کنند.
• مثال: اگر بدانیم فلان نتیجه در پایان حتماً رخ خواهد داد، می‌توانیم رفتارهای قبل از آن را تبیین کنیم.

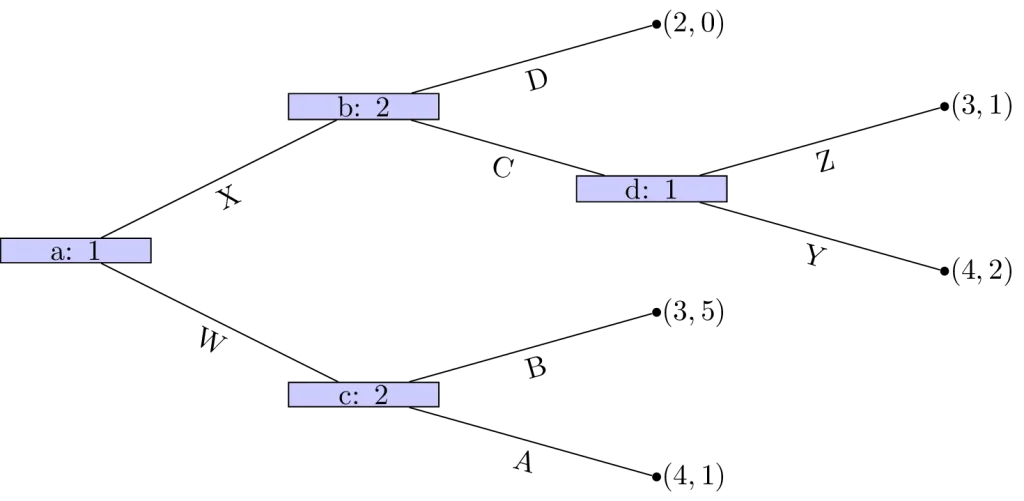
مراحل اجرای استقرا معکوس

برای استفاده از استقرا معکوس در یک مسئله، مراحل زیر معمولاً دنبال می‌شوند:

1. تعیین حالت‌های نهایی: ابتدا تمام نتایج ممکن در پایان بازی یا مسئله شناسایی می‌شوند.

2. محاسبه سود یا هزینه: برای هر حالت نهایی، سود یا هزینه مرتبط با آن برای بازیکنان یا تصمیم‌گیرندگان محاسبه می‌شود.

3. حرکت به مرحله قبلی: با فرض اینکه تصمیم‌گیرندگان در مرحله نهایی بهینه عمل می‌کنند، بهترین تصمیمات در مرحله قبل از آخر تعیین می‌شود.

4. تکرار فرآیند: این فرآیند به‌صورت بازگشتی تا رسیدن به مرحله اولیه ادامه می‌یابد.

5. استخراج استراتژی بهینه: در نهایت، استراتژی یا مسیر تصمیم‌گیری بهینه برای کل مسئله استخراج می‌شود.

مثال‌های عملی استقرا معکوس

مثال 1: بازی شطرنج

در شطرنج، استقرا معکوس در الگوریتم‌های کامپیوتری مانند Minimax استفاده می‌شود. فرض کنید در یک موقعیت خاص، تنها چند حرکت تا پایان بازی باقی مانده است. الگوریتم ابتدا تمام موقعیت‌های نهایی (مثل کیش‌ومات یا تساوی) را بررسی می‌کند، سپس به عقب برمی‌گردد و بهترین حرکت را در هر مرحله انتخاب می‌کند.

مثال 2: مذاکره تجاری

تصور کنید دو شرکت در حال مذاکره برای تقسیم سود یک پروژه هستند. اگر مذاکره در مرحله آخر به نتیجه نرسد، هر دو ضرر می‌کنند. با استفاده از استقرا معکوس، ابتدا نتایج شکست مذاکره بررسی می‌شود، سپس در هر مرحله از مذاکره، پیشنهادهایی که به حداکثر سود برای هر دو طرف منجر می‌شود، انتخاب می‌گردد.

مثال 3: برنامه‌ریزی پویا (مسئله کوله‌پشتی)

در مسئله کوله‌پشتی (Knapsack Problem)، استقرا معکوس می‌تواند برای تعیین بهترین ترکیب اقلام برای قرار دادن در کوله‌پشتی با ظرفیت محدود استفاده شود. با شروع از آخرین آیتم و حرکت به عقب، می‌توان تصمیم گرفت که کدام آیتم‌ها باید انتخاب شوند.

مزایای استقرا معکوس

• دقت بالا: در مسائل با اطلاعات کامل، این روش راه‌حل بهینه را تضمین می‌کند.
• ساختار منظم: استقرا معکوس یک روش سیستماتیک برای حل مسائل پیچیده ارائه می‌دهد.
• کاربرد گسترده: این روش در حوزه‌های مختلف از ریاضیات تا علوم اجتماعی قابل استفاده است.
• کاهش پیچیدگی: با تجزیه مسئله به مراحل کوچکتر، حل مسائل بزرگ ساده‌تر می‌شود.

محدودیت‌های استقرا معکوس

• نیاز به اطلاعات کامل: این روش در بازی‌هایی با اطلاعات ناقص (Imperfect Information) یا عدم قطعیت زیاد کارایی کمتری دارد.
• پیچیدگی محاسباتی: در مسائل با تعداد زیاد مراحل یا حالت‌ها، محاسبات ممکن است بسیار زمان‌بر شوند.
• فرض عقلانیت کامل: استقرا معکوس فرض می‌کند که همه بازیکنان یا تصمیم‌گیرندگان کاملاً منطقی عمل می‌کنند، که در دنیای واقعی همیشه صادق نیست.
• محدودیت در مقیاس‌پذیری: در مسائل بسیار بزرگ، مانند بازی‌های پیچیده با تعداد زیادی بازیکن، استفاده از این روش دشوار است.

تفاوت استقرا معکوس با استقرا رو به جلو

استقرا رو به جلو (Forward Induction) از نقطه شروع مسئله آغاز می‌شود و با پیش‌بینی نتایج ممکن، به سمت جلو حرکت می‌کند. این روش معمولاً در مسائل با اطلاعات ناقص یا زمانی که پیش‌بینی رفتار بازیکنان دشوار است، استفاده می‌شود. در مقابل، استقرا معکوس از پایان شروع می‌کند و به عقب برمی‌گردد، که آن را برای مسائل با اطلاعات کامل مناسب‌تر می‌کند.

جمع‌بندی

استقرا معکوس (بازگشت به عقب) روشی برای حل مسائل و اثبات قضایا از پایان به آغاز است. این روش به‌ویژه در نظریه بازی‌ها، اقتصاد رفتاری، علوم کامپیوتر و ریاضیات نقش کلیدی دارد. ایده اصلی این است:

اگر بدانیم در پایان چه اتفاقی می‌افتد، می‌توانیم تصمیمات و استدلال‌های قبل از آن را پیش‌بینی کنیم.

به بیان ساده، گاهی برای فهمیدن اینکه در ابتدا چه باید کرد، باید از پایان شروع کنیم.

سوالات متداول

۱. استقرا معکوس چه تفاوتی با استقرا معمولی دارد؟

در استقرا معمولی از حالت پایه (مثلاً (n=1)) شروع می‌کنیم و به جلو می‌رویم، اما در استقرا معکوس از حالت پایانی شروع کرده و به عقب برمی‌گردیم.

۲. آیا استقرا معکوس فقط در ریاضیات استفاده می‌شود؟

خیر. علاوه بر ریاضیات، در علوم کامپیوتر، نظریه بازی‌ها، اقتصاد، منطق و حتی فلسفه هم کاربرد دارد.

۳. در نظریه بازی‌ها چرا از بازگشت به عقب استفاده می‌کنیم؟

چون در بازی‌های ترتیبی باید تصمیم‌های بازیگران را از انتهای بازی تحلیل کنیم. هر بازیکن پیش‌بینی می‌کند که حریف در آینده چه کاری انجام می‌دهد و بر اساس آن تصمیم می‌گیرد.

۴. آیا استقرا معکوس همیشه جواب می‌دهد؟

نه لزوماً. این روش زمانی کارآمد است که:

• نقطه پایان مشخص باشد.
• تعداد مراحل محدود باشد.
• بازیگران یا عوامل به‌طور عقلانی تصمیم بگیرند.

۵. چه ارتباطی بین استقرا معکوس و الگوریتم‌ها وجود دارد؟

بسیاری از الگوریتم‌های بازگشتی و برنامه‌نویسی پویا (Dynamic Programming) بر پایه استقرا معکوس طراحی می‌شوند. به جای شروع از ابتدا، مسئله از پایان به ابتدای آن بازسازی می‌شود.

۶. یک مثال معروف از استقرا معکوس چیست؟

مثال “بازی تقسیم پول” یا “تقسیم کیک”: اگر دو نفر بخواهند پولی را بین خود تقسیم کنند و می‌دانند که در مرحله آخر یکی از آنها می‌تواند تمام پول را برای خود بردارد، از همان ابتدای بازی بر اساس این نتیجه تصمیم می‌گیرند.

۷. چرا به استقرا معکوس، بازگشت به عقب هم می‌گویند؟

چون در این روش تحلیل و استدلال از آخر به اول انجام می‌شود؛ درست مثل کسی که یک فیلم را از آخر به عقب نگاه کند تا بفهمد ابتدا چه اتفاقی افتاده است.

۸. آیا استقرا معکوس همیشه ساده‌تر از استقرا مستقیم است؟

نه. گاهی استقرا مستقیم ساده‌تر است، اما در بسیاری از مسائل ترتیبی و تصمیم‌گیری، بازگشت به عقب بهترین و گاهی تنها روش ممکن است.